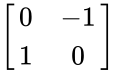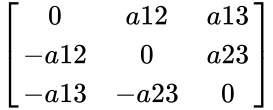Difference between revisions of "Manuals/calci/ANTISYMMETRIC"
Jump to navigation
Jump to search
| Line 63: | Line 63: | ||
| 7 || -93 || 58 || 83 ||0 | | 7 || -93 || 58 || 83 ||0 | ||
|} | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|JCT3EaVLUeo|280|center|Symmetric Matrices}} | ||
==See Also== | ==See Also== | ||
Revision as of 13:36, 25 July 2015
MATRIX("ANTISYMMETRIC",order)
- is the order of the Anti diagonal matrix.
Description
- This function gives the matrix of order 3 which is satisfying the anti symmetric properties.
- An antisymmetric matrix is a square matrix that satisfies the identity A=-A^(T) ,where A^(T) is the matrix transpose.
- For example, A=
- So the form of anti symmetric is
- Antisymmetric matrices are commonly called "skew symmetric matrices" or "antimetric".
- So in CALCI,users can give the syntax as:
- 1.MATRIX("anti-symmetric")
- 2.MATRIX("antisymmetric")
- 2.MATRIX("skewsymmetric")
- 3.MATRIX("skew-symmetric)
- Here this is case-insensitive.
Examples
- MATRIX("antisymmetric")
| 0 | 50 | -87 |
| -50 | 0 | 12 |
| 87 | -12 | 0 |
- MATRIX("anti-symmetric",4)
| 0 | 31 | -41 | -44 |
| -31 | 0 | 67 | -88 |
| 41 | -67 | 0 | 100 |
| 44 | 88 | -100 | 0 |
- MATRIX("skewsymmetric",2)
| 0 | -78 |
| 78 | 0 |
- MATRIX("skew-symmetric",5)
| 0 | 34 | -3 | 79 | -7 |
| -34 | 0 | 94 | 81 | 93 |
| 3 | -94 | 0 | 81 | -58 |
| -79 | -81 | -81 | 0 | -83 |
| 7 | -93 | 58 | 83 | 0 |
 is the order of the Anti diagonal matrix.
is the order of the Anti diagonal matrix.