Difference between revisions of "Manuals/calci/TTESTTWOSAMPLESEQUALVARIANCES"
Jump to navigation
Jump to search
| Line 38: | Line 38: | ||
|} | |} | ||
| − | #=TTESTTWOSAMPLESEQUALVARIANCES(A1:F1,A2:F2,2,0.5,1) | + | #=TTESTTWOSAMPLESEQUALVARIANCES(A1:F1,A2:F2,2,0.5,0) |
| + | {| class="wikitable" | ||
| + | |+t-Test: Two-Sample Assuming Equal Variances | ||
| + | |- | ||
| + | ! !! Variable 1 !! Variable 2 | ||
| + | |- | ||
| + | ! Mean | ||
| + | | 19.333333333333332 || 20.666666666666668 | ||
| + | |- | ||
| + | ! Variance | ||
| + | | 87.06666666666666 || 109.86666666666667 | ||
| + | |- | ||
| + | ! Observations | ||
| + | | 6 || 6 | ||
| + | |- | ||
| + | ! Pooled Variance | ||
| + | | 98.46666666666667 | ||
| + | |- | ||
| + | ! Hypothesized Mean Difference | ||
| + | | 2 | ||
| + | |- | ||
| + | ! Degree Of Freedom | ||
| + | | 10 | ||
| + | |- | ||
| + | ! T- Statistics | ||
| + | | -0.5818281835787091 | ||
| + | |- | ||
| + | ! P(T<=t) One-tail | ||
| + | | 0.28678199670723614 | ||
| + | |- | ||
| + | ! T Critical One-Tail | ||
| + | | 0 | ||
| + | |- | ||
| + | ! P(T<=t) Two-tail | ||
| + | | 0.5735639934144723 | ||
| + | |- | ||
| + | ! T Critical Two-Tail | ||
| + | | 0.6998120613365443 | ||
| + | |} | ||
==See Also== | ==See Also== | ||
Revision as of 15:34, 22 December 2016
TTESTTWOSAMPLESEQUALVARIANCES (Array1,Array2,HypothesizedMeanDifference,Alpha,NewTableFlag)
- and are set of values.
- is the Hypothesized Mean Difference.
- is the significance level.
- is either 0 or 1.
Description
- This function calculating the two Sample for equal variances determines whether two sample means are equal.
- We can use this test when both:
- 1.The two sample sizes are equal;
- 2.It can be assumed that the two distributions have the same variance.
- In , and are two arrays of sample values. is the Hypothesized Mean Difference .
- Suppose HypothesizedMeanDifference=0 which indicates that sample means are hypothesized to be equal.
- is the significance level which ranges from 0 to 1.
- is either 0 or 1.
- "1" is indicating the result will display in new worksheet.Suppose we are omitted the NewTableFlag value it will consider the value as "0".
- The t statistic of this function calculated by:
where
- Here and are unbiased estimators of the variances of two samples. is the grand standard deviation data 1 and data2 and n is the data points of two data set.
- This function will give the result as error when
1.any one of the argument is non-numeric. 2.Alpha>1 3. and are having different number of data points.
Examples
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 10 | 15 | 18 | 27 | 12 | 34 |
| 2 | 17 | 20 | 25 | 39 | 9 | 14 |
- =TTESTTWOSAMPLESEQUALVARIANCES(A1:F1,A2:F2,2,0.5,0)
| Variable 1 | Variable 2 | |
|---|---|---|
| Mean | 19.333333333333332 | 20.666666666666668 |
| Variance | 87.06666666666666 | 109.86666666666667 |
| Observations | 6 | 6 |
| Pooled Variance | 98.46666666666667 | |
| Hypothesized Mean Difference | 2 | |
| Degree Of Freedom | 10 | |
| T- Statistics | -0.5818281835787091 | |
| P(T<=t) One-tail | 0.28678199670723614 | |
| T Critical One-Tail | 0 | |
| P(T<=t) Two-tail | 0.5735639934144723 | |
| T Critical Two-Tail | 0.6998120613365443 |
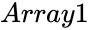 and
and 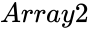 are set of values.
are set of values.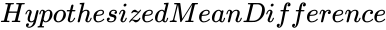 is the Hypothesized Mean Difference.
is the Hypothesized Mean Difference.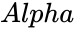 is the significance level.
is the significance level.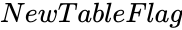 is either 0 or 1.
is either 0 or 1.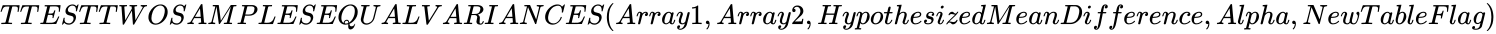 ,
, 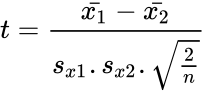
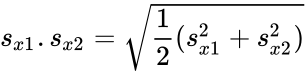
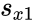 and
and 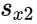 are unbiased estimators of the variances of two samples.
are unbiased estimators of the variances of two samples.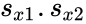 is the grand standard deviation data 1 and data2 and n is the data points of two data set.
is the grand standard deviation data 1 and data2 and n is the data points of two data set.