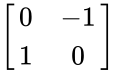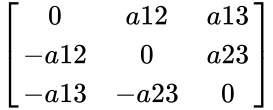Difference between revisions of "Manuals/calci/ANTISYMMETRIC"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''ANTISYMMETRIC'''</div><br/>") |
|||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''ANTISYMMETRIC'''</div><br/> | + | <div style="font-size:30px">'''MATRIX("ANTISYMMETRIC",order)'''</div><br/> |
| + | *<math> order </math> is the order of the Anti diagonal matrix. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the matrix of order 3 which is satisfying the anti symmetric properties. | ||
| + | *An antisymmetric matrix is a square matrix that satisfies the identity A=-A^(T) ,where A^(T) is the matrix transpose. | ||
| + | *For example, A= <math>\begin{bmatrix} | ||
| + | 0 & -1 \\ | ||
| + | 1 & 0 \\ | ||
| + | \end{bmatrix}</math> | ||
| + | *So the form of anti symmetric is <math>\begin{bmatrix} | ||
| + | 0 & a12 & a13 \\ | ||
| + | -a12 & 0 & a23 \\ | ||
| + | -a13 & -a23 & 0 \\ | ||
| + | \end{bmatrix}</math> | ||
| + | *Antisymmetric matrices are commonly called "skew symmetric matrices" or "antimetric". | ||
| + | *So in CALCI,users can give the syntax as: | ||
| + | *1.MATRIX("anti-symmetric") | ||
| + | *2.MATRIX("antisymmetric") | ||
| + | *2.MATRIX("skewsymmetric") | ||
| + | *3.MATRIX("skew-symmetric") | ||
| + | *Here this is case-insensitive. | ||
| + | |||
| + | ==Examples== | ||
| + | *MATRIX("antisymmetric",3) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 0 || 50 || -87 | ||
| + | |- | ||
| + | | -50 || 0 || 12 | ||
| + | |- | ||
| + | | 87 || -12 || 0 | ||
| + | |} | ||
| + | *MATRIX("anti-symmetric",4) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 0 || 31 || -41 || -44 | ||
| + | |- | ||
| + | | -31 || 0 || 67 || -88 | ||
| + | |- | ||
| + | | 41 || -67 || 0 || 100 | ||
| + | |- | ||
| + | | 44 || 88 || -100 || 0 | ||
| + | |} | ||
| + | *MATRIX("skewsymmetric",2) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 0 || -78 | ||
| + | |- | ||
| + | | 78 || 0 | ||
| + | |} | ||
| + | *MATRIX("skew-symmetric",5) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 0 || 34 || -3 || 79 || -7 | ||
| + | |- | ||
| + | | -34 || 0 || 94 || 81 || 93 | ||
| + | |- | ||
| + | | 3 || -94 || 0 || 81 || -58 | ||
| + | |- | ||
| + | | -79 || -81 || -81 || 0 || -83 | ||
| + | |- | ||
| + | | 7 || -93 || 58 || 83 ||0 | ||
| + | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|JCT3EaVLUeo|280|center|Symmetric Matrices}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/ARROWHEAD| ARROWHEAD]] | ||
| + | *[[Manuals/calci/ANTIDIAGONAL| ANTIDIAGONAL]] | ||
| + | *[[Manuals/calci/MATRIXOPERATORS| MATRIXOPERATORS]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Skew-symmetric_matrix Skew Symmetric] | ||
Latest revision as of 13:45, 30 January 2017
MATRIX("ANTISYMMETRIC",order)
- is the order of the Anti diagonal matrix.
Description
- This function gives the matrix of order 3 which is satisfying the anti symmetric properties.
- An antisymmetric matrix is a square matrix that satisfies the identity A=-A^(T) ,where A^(T) is the matrix transpose.
- For example, A=
- So the form of anti symmetric is
- Antisymmetric matrices are commonly called "skew symmetric matrices" or "antimetric".
- So in CALCI,users can give the syntax as:
- 1.MATRIX("anti-symmetric")
- 2.MATRIX("antisymmetric")
- 2.MATRIX("skewsymmetric")
- 3.MATRIX("skew-symmetric")
- Here this is case-insensitive.
Examples
- MATRIX("antisymmetric",3)
| 0 | 50 | -87 |
| -50 | 0 | 12 |
| 87 | -12 | 0 |
- MATRIX("anti-symmetric",4)
| 0 | 31 | -41 | -44 |
| -31 | 0 | 67 | -88 |
| 41 | -67 | 0 | 100 |
| 44 | 88 | -100 | 0 |
- MATRIX("skewsymmetric",2)
| 0 | -78 |
| 78 | 0 |
- MATRIX("skew-symmetric",5)
| 0 | 34 | -3 | 79 | -7 |
| -34 | 0 | 94 | 81 | 93 |
| 3 | -94 | 0 | 81 | -58 |
| -79 | -81 | -81 | 0 | -83 |
| 7 | -93 | 58 | 83 | 0 |
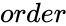 is the order of the Anti diagonal matrix.
is the order of the Anti diagonal matrix.