Difference between revisions of "Manuals/calci/CORRELATIONDATAANALYSIS"
Jump to navigation
Jump to search
| Line 16: | Line 16: | ||
==Examples== | ==Examples== | ||
| − | #CORRELATIONDATAANALYSIS([ | + | #CORRELATIONDATAANALYSIS([[56,56,65,65,50,25,87,44,35],[87,91,85,91,75,28,122,66,58]],"rows",1) |
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! CORRELATION BY ROWS | ||
| + | |- | ||
| + | ! !! ROW1 !!ROW2 | ||
| + | |- | ||
| + | | ROW1 || 1 || 0.9661943464912911 | ||
| + | |- | ||
| + | |ROW2 || 0.9661943464912911 || 1 | ||
| + | |} | ||
| + | |||
| + | |||
| + | 1 | ||
| + | 1 | ||
==See Also== | ==See Also== | ||
Revision as of 18:29, 13 February 2017
CORRELATIONDATAANALYSIS (Array,GroupBy,NewTableFlag)
- is the set of numbers
- is the group name.
- is either 0 or 1.
Description
- This function shows the correlation data analysis.
- The Correlation coeffiecient shows the relationship between two continuous variables of each other.
- In , is the set of numbers .
- is the group name of correlation and is either "0" or"1".
- We can use the CORREL function to find the correlation coefficient between two variables.
- This is also called Pearson's correlation coefficient.
- It is a measure of the strength of the association between the two variables.
- The correlation coefficient should not be calculated if the relationship is not linear.
- Positive correlation indicates that both variables increase or decrease together, whereas negative correlation indicates that as one variable increases, so the other decreases, and vice versa.
Examples
- CORRELATIONDATAANALYSIS([[56,56,65,65,50,25,87,44,35],[87,91,85,91,75,28,122,66,58]],"rows",1)
| CORRELATION BY ROWS | ||
|---|---|---|
| ROW1 | ROW2 | |
| ROW1 | 1 | 0.9661943464912911 |
| ROW2 | 0.9661943464912911 | 1 |
1
1
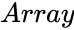 is the set of numbers
is the set of numbers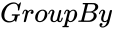 is the group name.
is the group name.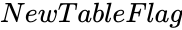 is either 0 or 1.
is either 0 or 1.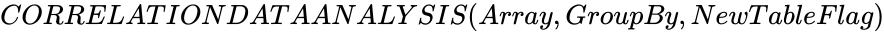 ,
, is the group name of correlation and
is the group name of correlation and  is either "0" or"1".
is either "0" or"1".