Difference between revisions of "Manuals/calci/ADJ"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''ADJ(Array)'''</div><br/> *<math>Array</math> is the set of values. ==Description== *This function shows the Adjoint of a given matrix. *In <mat...") |
|||
| Line 20: | Line 20: | ||
*Consider3x3 matrix <math>A=\begin{pmatrix} | *Consider3x3 matrix <math>A=\begin{pmatrix} | ||
a_{11} & a_{12} & a_{13} \\ | a_{11} & a_{12} & a_{13} \\ | ||
| − | + | a_{21} & a_{22} & a_{23} \\ | |
| − | \end{pmatrix} </math> | + | a_{31} & a_{32} & a_{33} |
| − | + | \end{pmatrix} </math>. | |
| − | + | *Its adjugate is the transpose of its cofactor matrix:<math>adj(A)=C^{T} = | |
| + | \begin{pmatrix} | ||
| + | +\begin{vmatrix} | ||
| + | a_ {22}& a_{23} \\ | ||
| + | a_ {32}& a_{33} | ||
| + | \end{vmatrix} & - \begin{vmatrix} | ||
| + | a_ {12}& a_{13} \\ | ||
| + | a_ {32}& a_{33} | ||
| + | \end{vmatrix} & +\begin{vmatrix} | ||
| + | a_ {12}& a_{13} \\ | ||
| + | a_ {22}& a_{23} | ||
| + | \end{vmatrix}</math> | ||
| + | a_{12} & a_{13} \\ | ||
| + | a_{21} & a_{22} & a_{23} \\ | ||
| + | a_{31} & a_{32} & a_{33} | ||
| + | \end{pmatrix} </math>. | ||
==References== | ==References== | ||
*[https://en.wikipedia.org/wiki/Adjugate_matrix Adjugate matrix] | *[https://en.wikipedia.org/wiki/Adjugate_matrix Adjugate matrix] | ||
Revision as of 13:45, 1 June 2017
ADJ(Array)
- is the set of values.
Description
- This function shows the Adjoint of a given matrix.
- In , is the set of matrix values.
- Adjoint of a matrix is called adjugate, classical adjoint, or adjunct.Adjoint of a matrix formed by taking the transpose of the cofactor matrix of a given original Square matrix.
- Adjoint of matrix A is written by .
- The adjugate of A is the transpose of the cofactor matrix C of A, .
- Also adjoint of a matrix is defined by .
- The adjugate of 1x1 matrix is .
- The adjugate of 2x2 matrix is .
- Consider3x3 matrix .
- Its adjugate is the transpose of its cofactor matrix:Failed to parse (unknown function "\begin{pmatrix}"): {\displaystyle adj(A)=C^{T} = \begin{pmatrix} +\begin{vmatrix} a_ {22}& a_{23} \\ a_ {32}& a_{33} \end{vmatrix} & - \begin{vmatrix} a_ {12}& a_{13} \\ a_ {32}& a_{33} \end{vmatrix} & +\begin{vmatrix} a_ {12}& a_{13} \\ a_ {22}& a_{23} \end{vmatrix}}
a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} </math>.
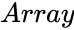 is the set of values.
is the set of values.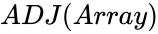 ,
,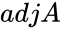 .
.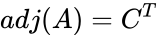 .
.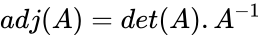 .
. .
.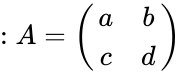 is
is 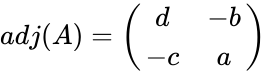 .
. .
.