Difference between revisions of "Manuals/calci/ADJ"
Jump to navigation
Jump to search
| Line 60: | Line 60: | ||
1.adj([[10,12],[-14,21]]) | 1.adj([[10,12],[-14,21]]) | ||
{| class="wikitable" | {| class="wikitable" | ||
| − | |||
|- | |- | ||
| 21 ||-12 | | 21 ||-12 | ||
| Line 68: | Line 67: | ||
2.adj([[4,5,8],[3,-6,-9],[10,-12,4]]) | 2.adj([[4,5,8],[3,-6,-9],[10,-12,4]]) | ||
{| class="wikitable" | {| class="wikitable" | ||
| − | |||
|- | |- | ||
| -132 ||-116||2.9999999999999982 | | -132 ||-116||2.9999999999999982 | ||
| Line 79: | Line 77: | ||
3.adj([[5,-2,2,7],[1,0,0,3], [-3,1,5,0], [3,-1,-9,4]]) | 3.adj([[5,-2,2,7],[1,0,0,3], [-3,1,5,0], [3,-1,-9,4]]) | ||
{| class="wikitable" | {| class="wikitable" | ||
| − | |||
|- | |- | ||
| -12 ||76||-60 ||-36 | | -12 ||76||-60 ||-36 | ||
Revision as of 14:06, 1 June 2017
ADJ(Array)
- is the set of values.
Description
- This function shows the Adjoint of a given matrix.
- In , is the set of matrix values.
- Adjoint of a matrix is called adjugate, classical adjoint, or adjunct.Adjoint of a matrix formed by taking the transpose of the cofactor matrix of a given original Square matrix.
- Adjoint of matrix A is written by .
- The adjugate of A is the transpose of the cofactor matrix C of A, .
- Also adjoint of a matrix is defined by .
- The adjugate of 1x1 matrix is .
- The adjugate of 2x2 matrix is .
- Consider3x3 matrix .
- Its adjugate is the transpose of its cofactor matrix:
Examples
1.adj([[10,12],[-14,21]])
| 21 | -12 |
| 14 | 10 |
2.adj([[4,5,8],[3,-6,-9],[10,-12,4]])
| -132 | -116 | 2.9999999999999982 |
| -102 | -64 | 60 |
| 24 | 98 | -39 |
3.adj([[5,-2,2,7],[1,0,0,3], [-3,1,5,0], [3,-1,-9,4]])
| -12 | 76 | -60 | -36 | |
| -56 | 207.99999999999997 | -81.99999999999999 | -57.99999999999999 | |
| 4 | 3.999999999999999 | -1.9999999999999998 | -10 | |
| 4 | 3.9999999999999982 | 20 | 12 |
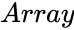 is the set of values.
is the set of values.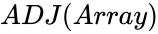 ,
,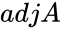 .
.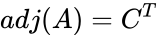 .
.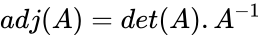 .
. .
.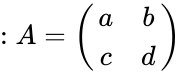 is
is 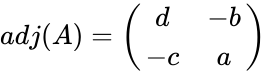 .
. .
.