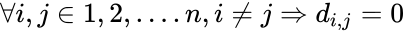Difference between revisions of "Manuals/calci/DIAGONALMATRIX"
Jump to navigation
Jump to search
| Line 16: | Line 16: | ||
*That is,the matrix D = (di,j) with n columns and n rows is diagonal if: | *That is,the matrix D = (di,j) with n columns and n rows is diagonal if: | ||
<math>\forall i,j \isin {1,2,....n},i \ne j \rArr d_{i,j} = 0</math> | <math>\forall i,j \isin {1,2,....n},i \ne j \rArr d_{i,j} = 0</math> | ||
| − | + | ||
| + | ==Examples== | ||
| + | |||
| + | ==See Also== | ||
| + | |||
| + | *[[Manuals/calci/DIAGONALFILL| DIAGONALFILL]] | ||
| + | *[[Manuals/calci/ARROWHEAD| ARROWHEAD]] | ||
| + | *[[Manuals/calci/MATRIXOPERATORS| MATRIXOPERATORS]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://mathworld.wolfram.com/DiagonalMatrix.html] | ||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Revision as of 13:11, 6 June 2017
DIAGONALMATRIX(Order)
- is the size or order of the matrix.
Description
- This function shows the Diagonal matrix of a given order.
- In , is the order of square matrix.
- A diagonal matrix is a square matrix which is of the form where is the Kronecker delta, are constants, and i,j=1, 2, ..., n.
- The general diagonal matrix is of the form:
- So the main diagonal entries are need not to be zero and off-diagonal entries are zero.
- That is,the matrix D = (di,j) with n columns and n rows is diagonal if:
Examples
See Also
References
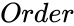 is the size or order of the matrix.
is the size or order of the matrix.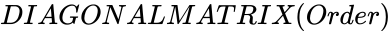 ,
, 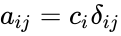 where
where 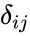 is the Kronecker delta,
is the Kronecker delta, 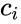 are constants, and i,j=1, 2, ..., n.
are constants, and i,j=1, 2, ..., n.