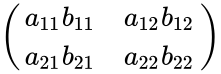Difference between revisions of "Manuals/calci/HADAMARDPRODUCT"
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
*Hadamard product is also called Schur product or entrywise product. | *Hadamard product is also called Schur product or entrywise product. | ||
*The Hadamard product is associative,commutative and distributive. | *The Hadamard product is associative,commutative and distributive. | ||
| − | *Hadamard product is defined by,For two matrices, A and B, of the same dimension, mxn, the Hadamard product, <math> A\circ B</math, is a matrix, of the same dimension as the operands, with elements given by: | + | *Hadamard product is defined by,For two matrices, A and B, of the same dimension, mxn, the Hadamard product, <math> A\circ B</math>, is a matrix, of the same dimension as the operands, with elements given by: |
<math>(A \circ B)_{i,j}=(A)_{i,j}(B)_{i,j} </math> | <math>(A \circ B)_{i,j}=(A)_{i,j}(B)_{i,j} </math> | ||
*Hadamard Product of order 2 is calculated by: | *Hadamard Product of order 2 is calculated by: | ||
Revision as of 13:28, 7 June 2017
HADAMARDPRODUCT (a,b)
- and are any two matrices.
Description
- This function shows the value of the Hadamard product.
- In , and are two matrices.
- Hadamard product is also called Schur product or entrywise product.
- The Hadamard product is associative,commutative and distributive.
- Hadamard product is defined by,For two matrices, A and B, of the same dimension, mxn, the Hadamard product, , is a matrix, of the same dimension as the operands, with elements given by:
- Hadamard Product of order 2 is calculated by:
=
 and
and  are any two matrices.
are any two matrices.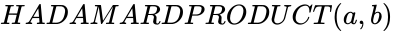 ,
,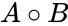 , is a matrix, of the same dimension as the operands, with elements given by:
, is a matrix, of the same dimension as the operands, with elements given by: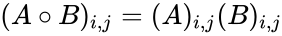
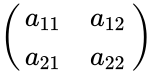

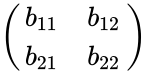 =
=