Manuals/calci/HADAMARDPRODUCT
- and are any two matrices.
Description
- This function shows the value of the Hadamard product.
- In , and are two matrices.
- Hadamard product is also called Schur product or entrywise product.
- The Hadamard product is associative,commutative and distributive.
- This product is the multiplied value of the each corresponding entries with the given two same dimension matrices.
- Hadamard product is defined by,For two matrices, A and B of the same dimension mxn, the Hadamard product Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\circ B} , is a matrix, of the same dimension as the operands, with elements given by:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (A \circ B)_{i,j}=(A)_{i,j}(B)_{i,j} }
- Hadamard Product of order 2 is calculated by:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \circ} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix}} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} a_{11}b_{11} & a_{12}b_{12} \\ a_{21}b_{21} & a_{22}b_{22} \end{pmatrix}}
Examples
1. HADAMARDPRODUCT([[2,3],[10,14]],[[6,4],[8,3]])
| 12 | 12 |
| 80 | 42 |
2. HADAMARDPRODUCT([[6,3,10],[5,-7,12],[4,2,6]],[[4,5,6],[9,2,-5],[12,13,7]])
| 24 | 15 | 60 |
| 45 | -14 | -60 |
| 48 | 26 | 42 |
Related Videos
See Also
References
 and
and  are any two matrices.
are any two matrices.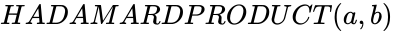 ,
,