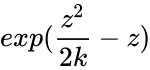Difference between revisions of "Manuals/calci/GFUNCTION"
Jump to navigation
Jump to search
| Line 10: | Line 10: | ||
*Formally, the Barnes G-function is defined in the following Weierstrass product form: | *Formally, the Barnes G-function is defined in the following Weierstrass product form: | ||
<math>G(1+z)={(2\pi)}^\frac{z}{2}exp(-\frac{z+z^2(1+\gamma)}{2})</math> | <math>G(1+z)={(2\pi)}^\frac{z}{2}exp(-\frac{z+z^2(1+\gamma)}{2})</math> | ||
| − | *<math>\prod_{k=1}^\infty | + | *<math>\prod_{k=1}^\infty [{(1+\frac{z}{k})}^k exp(\frac {z^2}{2k}-z)]</math> |
<math> exp(\frac {z^2}{2k}-z)</math> | <math> exp(\frac {z^2}{2k}-z)</math> | ||
{{(1+\frac{z}{k})}^k | {{(1+\frac{z}{k})}^k | ||
Revision as of 16:46, 8 August 2017
GFUNCTION (Number)
- is any positive real number.
Description
- This function shows the value of the Barnes G-function value.
- In , is any real number.
- is a function that is an extension of super factorials to the complex numbers.
- It is related to the Gamma function, the K-function and the Glaisher–Kinkelin constant, and was named after mathematician Ernest William Barnes.
- According to elementary factors, it is a special case of the double gamma function.
- Formally, the Barnes G-function is defined in the following Weierstrass product form:
{{(1+\frac{z}{k})}^k
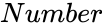 is any positive real number.
is any positive real number.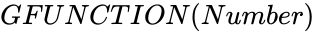 ,
,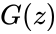 is a function that is an extension of super factorials to the complex numbers.
is a function that is an extension of super factorials to the complex numbers.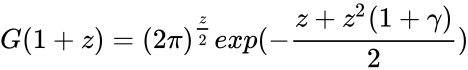
![{\displaystyle \prod _{k=1}^{\infty }[{(1+{\frac {z}{k}})}^{k}exp({\frac {z^{2}}{2k}}-z)]}](https://wikimedia.org/api/rest_v1/media/math/render/png/b6fbbae5c0bf9935e773aae90d6afb7f6fa675cd)