Difference between revisions of "Manuals/calci/MANDELBROT"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''MANDELBROT'''</div><br/> ==Description== *This function shows the figure of the Mandelbrot. *Fractals are infinitely complex patterns that are ...") |
|||
| Line 5: | Line 5: | ||
*Fractals are infinitely complex patterns that are self-similar across different scales. | *Fractals are infinitely complex patterns that are self-similar across different scales. | ||
*This property is called self-similarity. | *This property is called self-similarity. | ||
| − | *Fractals form a never ending pattern, created by repeating a simple process over and over, in an ongoing feedback loop.Mandelbrot Set is the set of points in the complex plane with the sequence <math>(c,c^2+c,{(c^2+c)}^2+c,{{((c^2+c)}^2+c)}^2+c, {{{(((c^2+c)}^2+c}^2+c)}^2+c,...)</math> where the result does not approach infinity. | + | *Fractals form a never ending pattern, created by repeating a simple process over and over, in an ongoing feedback loop.Mandelbrot Set is the set of points in the complex plane with the sequence <math>(c,c^2+c,{(c^2+c)}^2+c,{{((c^2+c)}^2+c)}^2+c, {{{(((c^2+c)}^2+c)}^2+c)}^2+c,...)</math> where the result does not approach infinity. |
*The Julia Set is closely related to Mandelbrot Set. | *The Julia Set is closely related to Mandelbrot Set. | ||
*The Mandelbrot Set is obtained from the quadratic recurrence equation <math>z_{n+1}={z_n}^2+c</math>, (with<math>z_0</math>=0), where points c in the complex plane for which the computed value of <math>z_n</math> does not tend to infinity. | *The Mandelbrot Set is obtained from the quadratic recurrence equation <math>z_{n+1}={z_n}^2+c</math>, (with<math>z_0</math>=0), where points c in the complex plane for which the computed value of <math>z_n</math> does not tend to infinity. | ||
Revision as of 16:49, 22 August 2017
MANDELBROT
Description
- This function shows the figure of the Mandelbrot.
- Fractals are infinitely complex patterns that are self-similar across different scales.
- This property is called self-similarity.
- Fractals form a never ending pattern, created by repeating a simple process over and over, in an ongoing feedback loop.Mandelbrot Set is the set of points in the complex plane with the sequence where the result does not approach infinity.
- The Julia Set is closely related to Mandelbrot Set.
- The Mandelbrot Set is obtained from the quadratic recurrence equation , (with=0), where points c in the complex plane for which the computed value of does not tend to infinity.
Examples
See Also
References
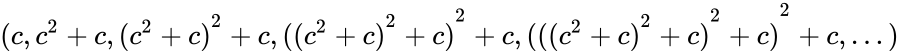 where the result does not approach infinity.
where the result does not approach infinity.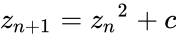 , (with
, (with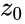 =0), where points c in the complex plane for which the computed value of
=0), where points c in the complex plane for which the computed value of 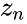 does not tend to infinity.
does not tend to infinity.