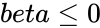Difference between revisions of "Manuals/calci/BETADISTX"
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
*The beta distribution is a family of Continuous Probability Distributions defined on the interval [0, 1] parameterized by two positive shape parameters, denoted by <math>\alpha</math> and <math>\beta</math>. | *The beta distribution is a family of Continuous Probability Distributions defined on the interval [0, 1] parameterized by two positive shape parameters, denoted by <math>\alpha</math> and <math>\beta</math>. | ||
*The Beta Distribution is also known as the Beta Distribution of the first kind. | *The Beta Distribution is also known as the Beta Distribution of the first kind. | ||
| − | *In <math>BETADISTX(x, | + | *In <math>BETADISTX(x,alpha,beta)</math>, <math>x</math> is any real number. |
*alpha is the value of the shape parameter. | *alpha is the value of the shape parameter. | ||
*beta is the value of the shape parameter | *beta is the value of the shape parameter | ||
| Line 16: | Line 16: | ||
*This function will give the result as error when | *This function will give the result as error when | ||
1.Any one of the arguments are non-numeric. | 1.Any one of the arguments are non-numeric. | ||
| − | 2.<math> | + | 2.<math>alpha \le 0</math> or <math>beta \le 0</math> |
==Examples== | ==Examples== | ||
Revision as of 16:21, 12 June 2018
BETADISTX(x,alpha,beta)
- is any real number.
- alpha and beta are the value of the shape parameter
Description
- This function gives the Cumulative Beta Probability Density function.
- The beta distribution is a family of Continuous Probability Distributions defined on the interval [0, 1] parameterized by two positive shape parameters, denoted by and .
- The Beta Distribution is also known as the Beta Distribution of the first kind.
- In , is any real number.
- alpha is the value of the shape parameter.
- beta is the value of the shape parameter
- The Probability Density Function of the beta distribution is:
where ; and is the Beta function.
- The formula for the Cumulative Beta Distribution is called the Incomplete Beta function ratio and it is denoted by and is defined as :
=, where ; and is the Beta function.
- This function will give the result as error when
1.Any one of the arguments are non-numeric. 2. or
Examples
- =BETADISTX(0.67,9,12) = 0.3102416743686678
- =BETADISTX(6,34,37) = 2.576888446568541e+72
- =BETADISTX(100,456,467)= NaN
See Also
References
 is any real number.
is any real number.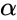 and
and 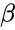 .
.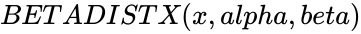 ,
, 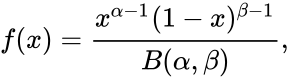 where
where  ;
; 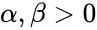 and
and 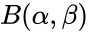 is the Beta function.
is the Beta function.
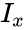 and is defined as :
and is defined as :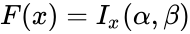 =
=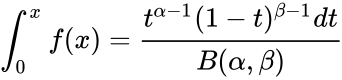 , where
, where  ;
; 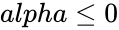 or
or