Difference between revisions of "Manuals/calci/MULTIPLEREGRESSIONANALYSIS"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
| − | <div style="font-size:25px">'''MULTIPLEREGRESSIONANALYSIS(yRange,xRange,ConfidenceLevel, | + | <div style="font-size:25px">'''MULTIPLEREGRESSIONANALYSIS(yRange,xRange,ConfidenceLevel,NewTableFlag)'''</div><br/> |
*<math>yRange</math> is the array of y-values. | *<math>yRange</math> is the array of y-values. | ||
*<math>xrange</math> is the array of x-values. | *<math>xrange</math> is the array of x-values. | ||
*<math>ConfidenceLevel</math> is the value betwen 0 and 1. | *<math>ConfidenceLevel</math> is the value betwen 0 and 1. | ||
| − | *<math> | + | *<math>NewTableFlag</math> is either TRUE or FALSE. |
==Description== | ==Description== | ||
Latest revision as of 13:19, 13 June 2018
MULTIPLEREGRESSIONANALYSIS(yRange,xRange,ConfidenceLevel,NewTableFlag)
- is the array of y-values.
- is the array of x-values.
- is the value betwen 0 and 1.
- is either TRUE or FALSE.
Description
- This function is calculating the Regression analysis of the given data for the multiple array of x values.
- The general purpose of multiple regression is to learn more about the relationship between several independent or predictor variables and a dependent or criterion variable.
- There are two types of Regressions.
1. Simple Regression. 2. Multiple Regression.
- 1.Simple Regression:.
- 2.Multiple regression:.
- The only difference between Simple Regression and Multiple Regression is there where one preditor or many.
- i.e., The difference is depending of the x-value.
- The Y is indicated as the "Dependent variable".
- The Predictor x is indicated as the "Independent Variable" .
- The output of a Regression statistics is of the form :
- Simple Regression:.
- Multiple Regression:.
- This analysis give the result in three table values.
1.Regression statistics table. 2.ANOVA table. 3.Residual output.
- 1.Regression statistics : It contains multiple R, R Square, Adjusted R Square, Standard Error and observations. R square gives the fittness of the data with the regression line.
- That value is closer to 1 is the better the regression line fits the data.
- Standard Error refers to the estimated standard deviation of the error term.
- It is called the standard error of the regression.
- 2.ANOVA table: ANOVA is the analysis of variance. This table splits in to two components which is Residual and Regression.
- Also this table gives the probability, T stat, significance of F and P for the each and every set of the data points.
- 3.Residual output: The residuals show you how far away the actual data points are fom the predicted data points.
- This table is displaying the values of Predicted data, Standard Residuals and Percentile value of the Y-value.
Examples
| A | B | C | |
|---|---|---|---|
| AGE | CHOLESTROL LEVEL | SUGAR LEVEL | |
| 1 | 58 | 189 | 136 |
| 2 | 69 | 235 | 149 |
| 3 | 43 | 198 | 165 |
| 4 | 39 | 137 | 140 |
| 5 | 63 | 178 | 162 |
| 6 | 52 | 160 | 152 |
| 7 | 47 | 198 | 142 |
| 8 | 31 | 183 | 129 |
- =MULTIPLEREGRESSIONANALYSIS(A1:A8,B1:C8,0.05,TRUE)
REGRESSION ANALYSIS OUTPUT
| Regression Statistics | |
|---|---|
| Multiple R | 0.6049214629315475 |
| R Square | 0.3659299763152436 |
| ADJUSTEDRSQUARE | 0.11230196684134108 |
| STANDARDERROR | 12.010450881972837 |
| OBSERVATIONS | 8 |
| DF | SS | MS | F | SIGNIFICANCE F | |
|---|---|---|---|---|---|
| REGRESSION | 2 | 416.24534805858957 | 208.12267402929479 | 1.442782195366701 | 0.3201422956953145 |
| RESIDUAL | 5 | 721.2546519414104 | 144.2509303882821 | ||
| TOTAL | 7 | 1137.5 |
| COEFFICIENTS | STANDARD ERROR | T STAT | P-VALUE | LOWER 95% | UPPER 95% | |
|---|---|---|---|---|---|---|
| INTERCEPT | -38.43476486203053 | 57.61581647557267 | -0.6670870468064214 | 0.5342620628633192 | -186.54092751432788 | 109.67139779026681 |
| INDEP1 | 0.19650498774518788 | 0.15890296267754417 | 1.2366351415608787 | 0.2711383732149726 | -0.211968057954515 | 0.6049780334448908 |
| INDEP2 | 0.3566329761773446 | 0.3665155982273022 | 0.973036285228361 | 0.3752244119102771 | -0.5855253082352574 | 1.2987912605899465 |
| OBSERVATION | PREDICTED Y | RESIDUALS | STANDARD RESIDUALS |
|---|---|---|---|
| 1 | -11.710086528684982 | 69.71008652868498 | 5.838810706001409 |
| 2 | -9.155521687997542 | 78.15552168799755 | 6.546187495797013 |
| 3 | -6.011441884074536 | 49.011441884074536 | 4.1051237466409525 |
| 4 | -10.924066577704231 | 49.92406657770423 | 4.181563801403094 |
| 5 | -6.600956847310098 | 69.6009568473101 | 5.829670170051966 |
| 6 | -8.566006724761976 | 60.566006724761976 | 5.072916504540229 |
| 7 | -10.531056602213855 | 57.53105660221385 | 4.8187137033369565 |
| 8 | -13.0856214429013 | 44.0856214429013 | 3.692544526617634 |
Related Videos
See Also
References
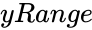 is the array of y-values.
is the array of y-values.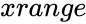 is the array of x-values.
is the array of x-values.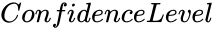 is the value betwen 0 and 1.
is the value betwen 0 and 1.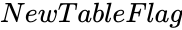 is either TRUE or FALSE.
is either TRUE or FALSE.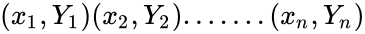 .
. .
.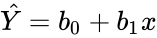 .
.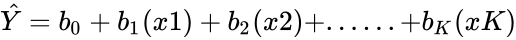 .
.