Difference between revisions of "Manuals/calci/IMLN"
Jump to navigation
Jump to search
| (17 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''IMLN( | + | <div style="font-size:30px">'''IMLN(Complexnumber)'''</div><br/> |
| − | *<math> | + | *<math>Complexnumber</math> is of the form <math>z=x+iy</math>. |
| + | **IMLN(),returns the natural logarithm of a complex number. | ||
| + | |||
==Description== | ==Description== | ||
| − | *This function gives the | + | *This function gives the Natural Logarithm of a complex number. |
| − | *In IMLN( | + | *In <math>IMLN(Complexnumber)</math>, where Complexnumber is in the form of <math>z=x+iy</math>. i.e <math>x</math> & <math>y</math> are the real numbers. |
| − | * | + | *And <math>I</math> is the imaginary unit <math>i=\sqrt{-1}</math>. |
| − | *A logarithm of z is a complex number w such that z = e^w and it is denoted by ln(z). | + | *Normally Complex logarithm function is an inverse of the Complex exponential function. |
| − | *If z = x+iy with x&y are real numbers then natural logarithm of a complex number : <math>ln(z)= w = ln(|z|) | + | *A logarithm of <math>z</math> is a complex number <math>w</math> such that <math>z = e^w</math> and it is denoted by <math>ln(z)</math>. |
| − | *We can use COMPLEX function to convert | + | *If <math>z = x+iy</math> with <math>x</math> & <math>y</math> are real numbers then natural logarithm of a complex number : |
| + | <math>ln(z)= w = ln(|z|) + iarg(z) = ln(\sqrt{x^2+y^2}+itan^{-1}(\frac{y}{x})</math> adding integer multiples of <math>2\pi i</math> gives all the others. | ||
| + | *We can use [[Manuals/calci/COMPLEX| COMPLEX]] function to convert real and imaginary number in to a complex number. | ||
| + | |||
| + | ==ZOS== | ||
| + | *The syntax is to calculate the natural logarithm of a complex number in ZOS is <math>IMLN(Complexnumber)</math>. | ||
| + | **<math>Complexnumber</math> is of the form <math>z=x+iy</math> | ||
| + | *For e.g.,IMLN("10+17i") | ||
| + | {{#ev:youtube|6JwQLlhPwi4|280|center|Natural Logarithm of a Complex Number}} | ||
| + | |||
==Examples== | ==Examples== | ||
#IMLN("3-2i")=1.28247467873077-0.588002603547568i | #IMLN("3-2i")=1.28247467873077-0.588002603547568i | ||
#IMLN("6+7i")=2.22132562824516+0.862170054667226i | #IMLN("6+7i")=2.22132562824516+0.862170054667226i | ||
| − | #IMLN("4")=1.38629436111989 | + | #IMLN("4")=1.38629436111989 +0i |
#IMLN("10i")=2.30258509299405+1.5707963267949i | #IMLN("10i")=2.30258509299405+1.5707963267949i | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|m-d_Xks90AM|280|center|Log of Complex Number}} | ||
==See Also== | ==See Also== | ||
| Line 20: | Line 35: | ||
*[[Manuals/calci/IMLOG2 | IMLOG2 ]] | *[[Manuals/calci/IMLOG2 | IMLOG2 ]] | ||
*[[Manuals/calci/COMPLEX | COMPLEX ]] | *[[Manuals/calci/COMPLEX | COMPLEX ]] | ||
| + | |||
| + | ==References== | ||
| + | [http://en.wikipedia.org/wiki/Imaginary_Logarithms Imaginary Logarithms] | ||
| − | + | ||
| − | [ | + | *[[Z_API_Functions | List of Main Z Functions]] |
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 15:30, 16 July 2018
IMLN(Complexnumber)
- is of the form .
- IMLN(),returns the natural logarithm of a complex number.
Description
- This function gives the Natural Logarithm of a complex number.
- In , where Complexnumber is in the form of . i.e & are the real numbers.
- And is the imaginary unit .
- Normally Complex logarithm function is an inverse of the Complex exponential function.
- A logarithm of is a complex number such that and it is denoted by .
- If with & are real numbers then natural logarithm of a complex number :
adding integer multiples of gives all the others.
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
ZOS
- The syntax is to calculate the natural logarithm of a complex number in ZOS is .
- is of the form
- For e.g.,IMLN("10+17i")
Examples
- IMLN("3-2i")=1.28247467873077-0.588002603547568i
- IMLN("6+7i")=2.22132562824516+0.862170054667226i
- IMLN("4")=1.38629436111989 +0i
- IMLN("10i")=2.30258509299405+1.5707963267949i
Related Videos
See Also
References
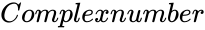 is of the form
is of the form 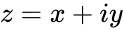 .
.
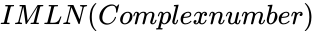 , where Complexnumber is in the form of
, where Complexnumber is in the form of  &
& 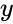 are the real numbers.
are the real numbers.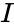 is the imaginary unit
is the imaginary unit 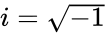 .
.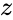 is a complex number
is a complex number 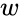 such that
such that 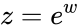 and it is denoted by
and it is denoted by 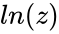 .
.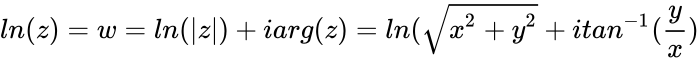 adding integer multiples of
adding integer multiples of 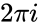 gives all the others.
gives all the others.