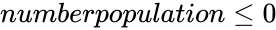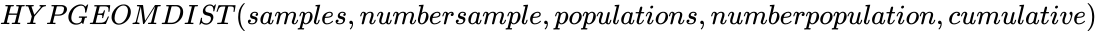Difference between revisions of "Manuals/calci/HYPGEOMDIST"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> <font face="Times New Roman">'''HYPGEOMDIST''' ('''n1, n2, n3, n4)'''</font> <font size="3"><font face="Times New ...") |
|||
| (25 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:20px">'''HYPGEOMDIST (sample_s,number_sample,population_s,number_population,cumulative)'''</div><br/> |
| + | *<math>samples</math> is the sample's success. | ||
| + | *<math>number sample</math> is the sample's size. | ||
| + | *<math>population s</math> is population's success. | ||
| + | *<math>number population</math> is the population size. | ||
| + | **HYPGEOMDIST(),returns the hypergeometric distribution. | ||
| − | + | ==Description== | |
| + | *This function gives the result of Hypergeometric Distribution. | ||
| + | *This distribution is a discrete probability distribution which is contrast to the binomial distribution. | ||
| + | *A Hypergeometric random variable is the number of successes that result from a Hypergeometric experiment. | ||
| + | *The probability distribution of a Hypergeometric random variable is called a Hypergeometric Distribution. | ||
| + | *In HYPGEOMDIST (sample_s,number_sample,population_s,number_population,cumulative) where samples is the number of items in the Sample that are classified as successes. | ||
| + | *<math>number sample</math> is the total number of items in the sample. | ||
| + | *<math>populations</math> is the number of items in the population that are classified as successes and <math>numberpopulation</math> is the total number of items in the sample. | ||
| + | *The following conditions are applied to the Hypergeometric distribution: | ||
| + | 1.This distribution is applies to sampling without replacement from a finite population whose elements can be | ||
| + | classified into two categories like Success or Failure. | ||
| + | 2.The population or set to be sampled consists of N individuals, objects,or elements | ||
| + | 3.Each individual can be success (S) or a failure (F), and there are M successes in the population. | ||
| + | 4.A sample of <math>n</math> individuals is selected without replacement in such a way that each subset of | ||
| + | size <math>n</math> is equally likely to be chosen. | ||
| + | *The Hyper geometric probability distribution is: | ||
| + | <math>\frac{\binom{m}{x} \binom{N-M}{n-x}}{\binom{m}{x}}</math> | ||
| + | for <math>x</math> is an integer satisfying <math>max(0, n-N+M)<=x<=min(n,M)</math>. where <math>x</math> is sample's success. | ||
| + | *<math>n</math> is the sample's size. | ||
| + | *<math>M</math> is population's success and <math>N</math> is the population size. | ||
| + | *Here we can give any positive real numbers. | ||
| + | *Suppose we are assigning any decimals numbers it will change in to Integers. | ||
| + | *This function will give result as error when | ||
| + | 1.Any one of the argument is non-numeric. | ||
| + | 2.<math>samples < 0</math> or samples is greater than the smaller value of numbersample or populations. | ||
| + | 3.<math>samples</math> is less than the bigger of 0 or(numbersample-numberpopulation+populations) | ||
| + | 4.<math>numbersample \le 0</math> or <math>numbersample>numberpopulation</math> | ||
| + | 5.<math>populations \le 0</math> or <math>populations>numberpopulation</math> or <math>numberpopulation \le 0</math> | ||
| − | < | + | ==ZOS== |
| + | *The syntax is to calculate HYPGEOMDIST in ZOS is <math>HYPGEOMDIST (sample s,number sample,population s,number population,cumulative) | ||
| + | </math> | ||
| + | **<math>sample s</math> is the sample's success. | ||
| + | **<math>number sample</math> is the sample's size. | ||
| + | **<math>population s</math> is population's success. | ||
| + | **<math>number population</math> is the population size. | ||
| + | *For e.g.,HYPGEOMDIST(2..3,6..7,9..10,20) | ||
| − | + | {{#ev:youtube|fui0xWgBO4g|280|center|Hyper-geometric Distribution}} | |
| − | + | ==Examples== | |
| − | + | #Draw 6 cards from a deck without replacement.What is the probability of getting two hearts? | |
| + | Here M = 13 number of hearts | ||
| + | N = 52 total number of cards | ||
| + | so N-M= 52-13= 39 and | ||
| + | x=2,n=6 so n-x=6-2=4 | ||
| + | =HYPGEOMDIST(2,6,13,52)=0.315129882 | ||
| + | #42 balls are numbered 1 - 42.You select six numbers between 1 and 42. What is the probability that they contain (i)match 3, (ii) match 4 | ||
| + | (i)Here M= 6,N=42,x=3and n=6 | ||
| + | HYPGEOMDIST(3,6,6,42)=0.02722185 | ||
| + | (ii)Here M= 6,N=42,x=4and n=6 | ||
| + | HYPGEOMDIST(4,6,6,42)=0.001801446 | ||
| − | + | ==Related Videos== | |
| − | + | {{#ev:youtube|NMeVWPdo7e4|280|center|Hyper-Geometric Distribution}} | |
| − | - | ||
| − | |||
| − | + | ==See Also== | |
| + | *[[Manuals/calci/BINOMDIST | BINOMDIST ]] | ||
| + | *[[Manuals/calci/COMBIN | COMBIN ]] | ||
| + | *[[Manuals/calci/FACT | FACT ]] | ||
| − | + | ==References== | |
| − | + | [http://en.wikipedia.org/wiki/Hypergeometric_distribution| Hypergeometric Distribution] | |
| − | |||
| − | |||
| − | |||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| − | + | *[[ Z3 | Z3 home ]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 16:19, 7 August 2018
HYPGEOMDIST (sample_s,number_sample,population_s,number_population,cumulative)
- is the sample's success.
- is the sample's size.
- is population's success.
- is the population size.
- HYPGEOMDIST(),returns the hypergeometric distribution.
Description
- This function gives the result of Hypergeometric Distribution.
- This distribution is a discrete probability distribution which is contrast to the binomial distribution.
- A Hypergeometric random variable is the number of successes that result from a Hypergeometric experiment.
- The probability distribution of a Hypergeometric random variable is called a Hypergeometric Distribution.
- In HYPGEOMDIST (sample_s,number_sample,population_s,number_population,cumulative) where samples is the number of items in the Sample that are classified as successes.
- is the total number of items in the sample.
- is the number of items in the population that are classified as successes and is the total number of items in the sample.
- The following conditions are applied to the Hypergeometric distribution:
1.This distribution is applies to sampling without replacement from a finite population whose elements can be classified into two categories like Success or Failure. 2.The population or set to be sampled consists of N individuals, objects,or elements 3.Each individual can be success (S) or a failure (F), and there are M successes in the population. 4.A sample of individuals is selected without replacement in such a way that each subset of size is equally likely to be chosen.
- The Hyper geometric probability distribution is:
for is an integer satisfying . where is sample's success.
- is the sample's size.
- is population's success and is the population size.
- Here we can give any positive real numbers.
- Suppose we are assigning any decimals numbers it will change in to Integers.
- This function will give result as error when
1.Any one of the argument is non-numeric. 2. or samples is greater than the smaller value of numbersample or populations. 3. is less than the bigger of 0 or(numbersample-numberpopulation+populations) 4. or 5. or or
ZOS
- The syntax is to calculate HYPGEOMDIST in ZOS is
- is the sample's success.
- is the sample's size.
- is population's success.
- is the population size.
- For e.g.,HYPGEOMDIST(2..3,6..7,9..10,20)
Examples
- Draw 6 cards from a deck without replacement.What is the probability of getting two hearts?
Here M = 13 number of hearts N = 52 total number of cards so N-M= 52-13= 39 and x=2,n=6 so n-x=6-2=4 =HYPGEOMDIST(2,6,13,52)=0.315129882
- 42 balls are numbered 1 - 42.You select six numbers between 1 and 42. What is the probability that they contain (i)match 3, (ii) match 4
(i)Here M= 6,N=42,x=3and n=6 HYPGEOMDIST(3,6,6,42)=0.02722185 (ii)Here M= 6,N=42,x=4and n=6 HYPGEOMDIST(4,6,6,42)=0.001801446
Related Videos
See Also
References
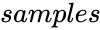 is the sample's success.
is the sample's success.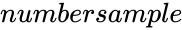 is the sample's size.
is the sample's size.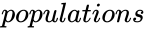 is population's success.
is population's success.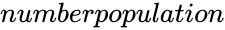 is the population size.
is the population size.
 individuals is selected without replacement in such a way that each subset of
size
individuals is selected without replacement in such a way that each subset of
size 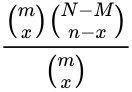 for
for  is an integer satisfying
is an integer satisfying 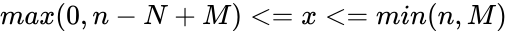 . where
. where 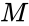 is population's success and
is population's success and 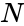 is the population size.
is the population size.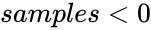 or samples is greater than the smaller value of numbersample or populations.
3.
or samples is greater than the smaller value of numbersample or populations.
3.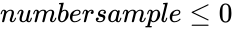 or
or 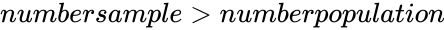 5.
5.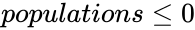 or
or 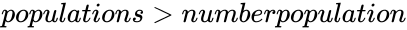 or
or