Difference between revisions of "Manuals/calci/STDEVIF"
Jump to navigation
Jump to search
| (2 intermediate revisions by the same user not shown) | |||
| Line 13: | Line 13: | ||
<math>S.D= \sqrt \frac {\sum(x-\bar{x})^2}{(n-1)} </math> | <math>S.D= \sqrt \frac {\sum(x-\bar{x})^2}{(n-1)} </math> | ||
where <math> \bar{x} </math> is the sample mean of <math> x </math> and <math> n </math> is the total numbers of the given data. | where <math> \bar{x} </math> is the sample mean of <math> x </math> and <math> n </math> is the total numbers of the given data. | ||
| − | *It is calculated using <math> | + | *It is calculated using <math>(n-1)</math> method. |
*This function is considering our given data is the sample of the population. | *This function is considering our given data is the sample of the population. | ||
*Suppose it should consider the data as the entire population, we can use the [[Manuals/calci/STDEVP | STDEVP ]] function. | *Suppose it should consider the data as the entire population, we can use the [[Manuals/calci/STDEVP | STDEVP ]] function. | ||
| Line 23: | Line 23: | ||
1. Any one of the argument is non-numeric. | 1. Any one of the argument is non-numeric. | ||
2. The arguments containing the error values or text that cannot be translated in to numbers | 2. The arguments containing the error values or text that cannot be translated in to numbers | ||
| + | |||
| + | ==Examples== | ||
| + | #STDEVIF([19,17,23,10,12,15,22],">10") = 4.1952353926806065 | ||
| + | #STDEVIF([22,24,27,32,10,18,45,43,55,14],"<15") = 2.8284271247461903 | ||
| + | #STDEVIF([22,24,27,32,10,18,45,43,55,14],">15") = 13.046619704516788 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=LZqQ4i-3WOk&t=217s|280|center|Standard Deviation IF}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/STDEV | STDEV]] | ||
| + | *[[Manuals/calci/STDEVP | STDEVP ]] | ||
| + | *[[Manuals/calci/STDEVA | STDEVA]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Standard_deviation Standard Deviation] | ||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 15:22, 30 November 2018
STDEVIF (Array,Condition,SumArray)
- is the set of values.
- is the particular condition value.
Description
- This function shows the Standard Deviation of the given set which satisfies the given condition.
- In , is the set of values.
- is the particular condition which satisfies the Standard deviation value.
- Standard Deviation is the quantity expressed by, how many members of a group differ from the mean value of the group.
- It is the used as a measure of the dispersion or variation in a distribution.
- It is calculated as the square root of variance.
is defined by the formula:
where is the sample mean of and is the total numbers of the given data.
- It is calculated using method.
- This function is considering our given data is the sample of the population.
- Suppose it should consider the data as the entire population, we can use the STDEVP function.
- The arguments can be be either numbers or names, array,constants or references that contain numbers.
- Suppose the array contains text,logical values or empty cells, like that values are not considered.
- When we are entering logical values and text representations of numbers as directly, then the arguments are counted.
- Suppose the function have to consider the logical values and text representations of numbers in a reference , we can use the STDEVA function.
- This function will return the result as error when
1. Any one of the argument is non-numeric.
2. The arguments containing the error values or text that cannot be translated in to numbers
Examples
- STDEVIF([19,17,23,10,12,15,22],">10") = 4.1952353926806065
- STDEVIF([22,24,27,32,10,18,45,43,55,14],"<15") = 2.8284271247461903
- STDEVIF([22,24,27,32,10,18,45,43,55,14],">15") = 13.046619704516788
Related Videos
See Also
References
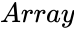 is the set of values.
is the set of values.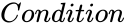 is the particular condition value.
is the particular condition value.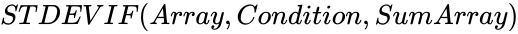 ,
,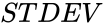 is defined by the formula:
is defined by the formula:
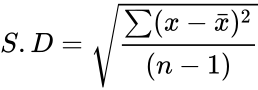
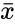 is the sample mean of
is the sample mean of  and
and  is the total numbers of the given data.
is the total numbers of the given data.
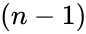 method.
method.