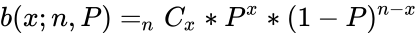Difference between revisions of "Manuals/calci/BINOMIALPROBABILTY"
Jump to navigation
Jump to search
(Created page with "==Feature==") |
|||
| Line 1: | Line 1: | ||
| − | == | + | <div style="font-size:30px">'''BINOMIALPROBABILTY (NumberOftrials,NumberOfSuccess,ProbabiltyOfSuccess)'''</div><br/> |
| + | *<math> | ||
| + | |||
| + | ==Description== | ||
| + | *This function shows the value of Binomial Probability. | ||
| + | *In <math>BINOMIALPROBABILTY (NumberOftrials,NumberOfSuccess,ProbabiltyOfSuccess)</math>,<math>NumberOf trials</math> is the number of times of the trials. | ||
| + | *<math>NumberofSuccess</math> is the results of the success. | ||
| + | *<math>ProbabilityOfSuccess</math> is the value of the Probability. | ||
| + | *The binomial probability refers to the probability that a binomial experiment results in exactly x successes. | ||
| + | *Suppose a binomial experiment consists of n trials and results in x successes. | ||
| + | *If the probability of success on an individual trial is P, then the binomial probability is: | ||
| + | <math>b(x; n, P) = _nC_x* P^x *(1 - P)^{n - x}</math> | ||
Revision as of 16:11, 27 December 2018
BINOMIALPROBABILTY (NumberOftrials,NumberOfSuccess,ProbabiltyOfSuccess)
- , is the number of times of the trials.
- is the results of the success.
- is the value of the Probability.
- The binomial probability refers to the probability that a binomial experiment results in exactly x successes.
- Suppose a binomial experiment consists of n trials and results in x successes.
- If the probability of success on an individual trial is P, then the binomial probability is:
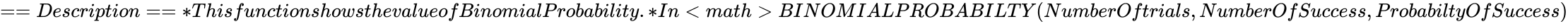 ,
,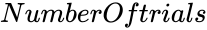 is the number of times of the trials.
is the number of times of the trials.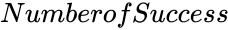 is the results of the success.
is the results of the success.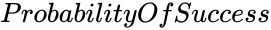 is the value of the Probability.
is the value of the Probability.