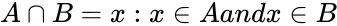Difference between revisions of "Manuals/calci/INTERSECTION"
Jump to navigation
Jump to search
| (2 intermediate revisions by the same user not shown) | |||
| Line 7: | Line 7: | ||
*The Intersection of two sets named as A and B is the set that contains all elements of A that also belong to B,but no other elements. | *The Intersection of two sets named as A and B is the set that contains all elements of A that also belong to B,but no other elements. | ||
*The intersection of A and B is written ""A ∩ B"". Formally: | *The intersection of A and B is written ""A ∩ B"". Formally: | ||
| − | <math>A\cap B= {x:x\isin A and x\isin B}</math> | + | <math>A\cap B= {x:x\isin A and x\isin B } </math> |
*This function will return the result as Null when there is no numbers or elements are in common. | *This function will return the result as Null when there is no numbers or elements are in common. | ||
| + | |||
| + | ==Examples== | ||
| + | #INTERSECTION([1,2,3,4],[2,4]) = 2 4 | ||
| + | #INTERSECTION([9,19,24,26,10,12,18,3,99],[24,20,99,8,12,10]) = 24 10 12 99 | ||
| + | #INTERSECTION([10.02,11.09,29.9,22.3,10.002,11.11,12.32],[10.002,11,29.9,13.01]) = 29.9 10.002 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=jAfNg3ylZAI|280|center|Intersection}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/UNION| UNION]] | ||
| + | *[[Manuals/calci/INTDIV| INTDIV]] | ||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | *[[ Z3 | Z3 home ]] | ||
| + | |||
| + | ==References== | ||
| + | [https://en.wikipedia.org/wiki/Intersection_(set_theory) Intersection] | ||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 14:39, 14 January 2019
INTERSECTION (GivenSet1,GivenSet2)
- and are any two set of values.
Description
- This function will return Common elements from the given two sets.
- In , and are any two set of numbers or any elements.
- The Intersection of two sets named as A and B is the set that contains all elements of A that also belong to B,but no other elements.
- The intersection of A and B is written ""A ∩ B"". Formally:
- This function will return the result as Null when there is no numbers or elements are in common.
Examples
- INTERSECTION([1,2,3,4],[2,4]) = 2 4
- INTERSECTION([9,19,24,26,10,12,18,3,99],[24,20,99,8,12,10]) = 24 10 12 99
- INTERSECTION([10.02,11.09,29.9,22.3,10.002,11.11,12.32],[10.002,11,29.9,13.01]) = 29.9 10.002
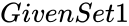 and
and 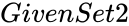 are any two set of values.
are any two set of values.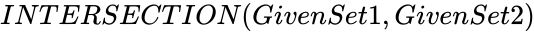 ,
,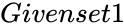 and
and 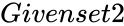 are any two set of numbers or any elements.
are any two set of numbers or any elements.