Difference between revisions of "Manuals/calci/MANDELBROT"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''MANDELBROT'''</div><br/> ==Description== *This function shows the figure of the Mandelbrot. *Fractals are infinitely complex patterns that are ...") |
|||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''MANDELBROT'''</div><br/> | + | <div style="font-size:30px">'''MANDELBROT (SettingsArray,Width,Height,MandeliterFunction,Shades,CanvasId)'''</div><br/> |
==Description== | ==Description== | ||
| Line 5: | Line 5: | ||
*Fractals are infinitely complex patterns that are self-similar across different scales. | *Fractals are infinitely complex patterns that are self-similar across different scales. | ||
*This property is called self-similarity. | *This property is called self-similarity. | ||
| − | *Fractals form a never ending pattern, created by repeating a simple process over and over, in an ongoing feedback loop.Mandelbrot Set is the set of points in the complex plane with the sequence <math>(c,c^2+c,{(c^2+c)}^2+c,{{((c^2+c)}^2+c)}^2+c, {{{(((c^2+c)}^2+c}^2+c)}^2+c,...)</math> where the result does not approach infinity. | + | *Fractals form a never ending pattern, created by repeating a simple process over and over, in an ongoing feedback loop.Mandelbrot Set is the set of points in the complex plane with the sequence <math>(c,c^2+c,{(c^2+c)}^2+c,{{((c^2+c)}^2+c)}^2+c, {{{(((c^2+c)}^2+c)}^2+c)}^2+c,...)</math> where the result does not approach infinity. |
*The Julia Set is closely related to Mandelbrot Set. | *The Julia Set is closely related to Mandelbrot Set. | ||
*The Mandelbrot Set is obtained from the quadratic recurrence equation <math>z_{n+1}={z_n}^2+c</math>, (with<math>z_0</math>=0), where points c in the complex plane for which the computed value of <math>z_n</math> does not tend to infinity. | *The Mandelbrot Set is obtained from the quadratic recurrence equation <math>z_{n+1}={z_n}^2+c</math>, (with<math>z_0</math>=0), where points c in the complex plane for which the computed value of <math>z_n</math> does not tend to infinity. | ||
==Examples== | ==Examples== | ||
| + | #MANDELBROT() | ||
| + | [[File:Mandelbrot.png]] | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=8ma6cV6fw24|280|center|Mandel brot}} | ||
| + | |||
==See Also== | ==See Also== | ||
| Line 15: | Line 22: | ||
*[[Manuals/calci/LISSAJOUSCURVE| LISSAJOUSCURVE ]] | *[[Manuals/calci/LISSAJOUSCURVE| LISSAJOUSCURVE ]] | ||
*[[Manuals/calci/LISSAJOUS| LISSAJOUS ]] | *[[Manuals/calci/LISSAJOUS| LISSAJOUS ]] | ||
| − | |||
==References== | ==References== | ||
Latest revision as of 14:47, 4 March 2019
MANDELBROT (SettingsArray,Width,Height,MandeliterFunction,Shades,CanvasId)
Description
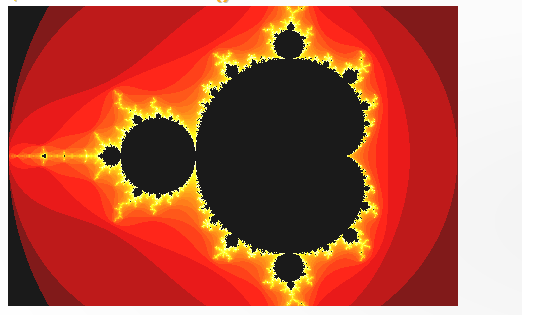
- This function shows the figure of the Mandelbrot.
- Fractals are infinitely complex patterns that are self-similar across different scales.
- This property is called self-similarity.
- Fractals form a never ending pattern, created by repeating a simple process over and over, in an ongoing feedback loop.Mandelbrot Set is the set of points in the complex plane with the sequence where the result does not approach infinity.
- The Julia Set is closely related to Mandelbrot Set.
- The Mandelbrot Set is obtained from the quadratic recurrence equation , (with=0), where points c in the complex plane for which the computed value of does not tend to infinity.
where the result does not approach infinity.
, (with
=0), where points c in the complex plane for which the computed value of 
does not tend to infinity.Examples
- MANDELBROT()
Related Videos
See Also
References