Difference between revisions of "Manuals/calci/MATRIXDIAGONALPRODUCT"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''MATRIXDIAGONALPRODUCT (a)'''</div><br/> *<math> a </math> is any square matrix. ==Description== *This function shows the product value of the m...") |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 10: | Line 10: | ||
*Here it is calculating the product of the main diagonal values. | *Here it is calculating the product of the main diagonal values. | ||
*So it is calculating <math>a_{11}*a_{22}*a_{33}</math> and so on. | *So it is calculating <math>a_{11}*a_{22}*a_{33}</math> and so on. | ||
| + | |||
| + | ==Examples== | ||
| + | # MATRIXDIAGONALPRODUCT([[5,8,12,13],[4,3,2,8],[7,2,5,3],[3,5,9,11]]) = 825 | ||
| + | # MATRIXDIAGONALPRODUCT([[1,2,3],[4,5,6],[9,8,6]]) = 30 | ||
| + | # MATRIXDIAGONALPRODUCT([[14,12],[13,15]]) = 210 | ||
| + | |||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=vzt9c7iWPxs|280|center|Matrix Multiplication}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/PRODUCT| PRODUCT]] | ||
| + | *[[Manuals/calci/ANTIDIAGONAL| ANTIDIAGONAL]] | ||
| + | *[[Manuals/calci/DIAGONALMATRIX| DIAGONALMATRIX ]] | ||
| + | |||
| + | ==References== | ||
| + | *[https://en.wikipedia.org/wiki/Main_diagonal Main diagonal] | ||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 13:49, 12 April 2019
MATRIXDIAGONALPRODUCT (a)
- is any square matrix.
Description
- This function shows the product value of the main diagonal values.
- In , is any square matrix.
- The main diagonal of a matrix consists of those elements that lie on the diagonal that runs from top left to bottom right.
- Main diagonal of a matrix A is defined by A is the collection of entries ,where i=j.
- So diagonal entries are and so on.
- Here it is calculating the product of the main diagonal values.
- So it is calculating and so on.
Examples
- MATRIXDIAGONALPRODUCT([[5,8,12,13],[4,3,2,8],[7,2,5,3],[3,5,9,11]]) = 825
- MATRIXDIAGONALPRODUCT([[1,2,3],[4,5,6],[9,8,6]]) = 30
- MATRIXDIAGONALPRODUCT([[14,12],[13,15]]) = 210
 is any square matrix.
is any square matrix.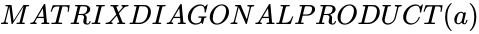 ,
, 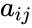 ,where i=j.
,where i=j.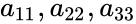 and so on.
and so on.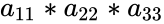 and so on.
and so on.