Difference between revisions of "Manuals/calci/EIGENVALUES"
Jump to navigation
Jump to search
| (13 intermediate revisions by 2 users not shown) | |||
| Line 5: | Line 5: | ||
*This function shows the Eigen value of the given matrix. | *This function shows the Eigen value of the given matrix. | ||
*In <math>EIGENVALUES (Matrix)</math>,<math>Matrix</math> is any matrix values. | *In <math>EIGENVALUES (Matrix)</math>,<math>Matrix</math> is any matrix values. | ||
| − | *In linear algebra,an eigen vector or characteristic vector of a linear transformation is a non-zero vector whose direction does not change when that linear transformation is applied to it. | + | *In linear algebra, an eigen vector or characteristic vector of a linear transformation is a non-zero vector whose direction does not change when that linear transformation is applied to it. |
*Let A be a linear transformation represented by a matrix A. | *Let A be a linear transformation represented by a matrix A. | ||
| − | *Let A is an nxn matrix,v is a non zero nx1 vector and <math>\ | + | *Let A is an nxn matrix, v is a non zero nx1 vector and <math>\lambda</math> is a scalar which may be either real or complex. |
| − | *Any value of <math>\ | + | *Any value of <math>\lambda</math> for which this equation has a solution is known as an eigenvalue of the matrix A. |
*It is sometimes also called the characteristic value. | *It is sometimes also called the characteristic value. | ||
*The vector, v, which corresponds to this value is called an eigenvector. | *The vector, v, which corresponds to this value is called an eigenvector. | ||
| − | *The eigenvalue problem can be rewritten as <math>(A-\ | + | *The eigenvalue problem can be rewritten as <math>(A-\lambda.I).v=0</math>. |
| − | *If v is non-zero, this equation will only have a solution if <math>|A-\ | + | *If v is non-zero, this equation will only have a solution if <math>|A-\lambda.I|.v=0</math>. |
| − | *This equation is called the characteristic equation of A, and is an nth order polynomial in <math>\ | + | *This equation is called the characteristic equation of A, and is an nth order polynomial in <math>\lambda</math> with n roots. |
*These roots are called the eigenvalues of A. | *These roots are called the eigenvalues of A. | ||
| + | |||
| + | ==Examples== | ||
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !! C | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 3 || 7 || 5 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 10 || 12 || 8 | ||
| + | |- | ||
| + | !3 | ||
| + | | 6 || 8 || 14 | ||
| + | |} | ||
| + | =EIGENVALUES(A1:C3) | ||
| + | {| border="1" cellpadding="5" cellspacing="0" | ||
| + | |- | ||
| + | | | ||
| + | -2.018987498930866 | ||
| + | || | ||
| + | 25.303239119591886 | ||
| + | || | ||
| + | 5.715748379338994 | ||
| + | |- | ||
| + | || | ||
| + | -0.8195524172935329 0.3557792393359474 0.2128903683040517 | ||
| + | || | ||
| + | 0.5726193656991498 0.663334322125492 0.6212592923173481 | ||
| + | || | ||
| + | 0.02099755544415341 0.6583378387635402 -0.7541316747045657 | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 5 || 6 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 9 || -11 | ||
| + | |} | ||
| + | =EIGENVALUES(A1:B2) | ||
| + | {| border="1" cellpadding="5" cellspacing="0" | ||
| + | |- | ||
| + | | | ||
| + | -13.862780491200214 | ||
| + | || | ||
| + | 7.8627804912002155 | ||
| + | |- | ||
| + | | | ||
| + | 0.3031213645114406 0.9025310769284506 | ||
| + | || | ||
| + | -0.9529519601620652 0.43062472662211493 | ||
| + | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=PhfbEr2btGQ|280|center|Eigen Values}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/ANTIDIAGONAL| ANTIDIAGONAL]] | ||
| + | *[[Manuals/calci/CONFERENCE| CONFERENCE]] | ||
| + | *[[Manuals/calci/PASCAL| PASCAL]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://lpsa.swarthmore.edu/MtrxVibe/EigMat/MatrixEigen.html Eigen Values] | ||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 13:58, 25 April 2019
EIGENVALUES (Matrix)
- is the array of numeric elements.
Description
- This function shows the Eigen value of the given matrix.
- In , is any matrix values.
- In linear algebra, an eigen vector or characteristic vector of a linear transformation is a non-zero vector whose direction does not change when that linear transformation is applied to it.
- Let A be a linear transformation represented by a matrix A.
- Let A is an nxn matrix, v is a non zero nx1 vector and is a scalar which may be either real or complex.
- Any value of for which this equation has a solution is known as an eigenvalue of the matrix A.
- It is sometimes also called the characteristic value.
- The vector, v, which corresponds to this value is called an eigenvector.
- The eigenvalue problem can be rewritten as .
- If v is non-zero, this equation will only have a solution if .
- This equation is called the characteristic equation of A, and is an nth order polynomial in with n roots.
- These roots are called the eigenvalues of A.
Examples
| A | B | C | |
|---|---|---|---|
| 1 | 3 | 7 | 5 |
| 2 | 10 | 12 | 8 |
| 3 | 6 | 8 | 14 |
=EIGENVALUES(A1:C3)
-2.018987498930866 |
25.303239119591886 |
5.715748379338994 |
-0.8195524172935329 0.3557792393359474 0.2128903683040517 |
0.5726193656991498 0.663334322125492 0.6212592923173481 |
0.02099755544415341 0.6583378387635402 -0.7541316747045657 |
| A | B | |
|---|---|---|
| 1 | 5 | 6 |
| 2 | 9 | -11 |
=EIGENVALUES(A1:B2)
-13.862780491200214 |
7.8627804912002155 |
0.3031213645114406 0.9025310769284506 |
-0.9529519601620652 0.43062472662211493 |
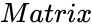 is the array of numeric elements.
is the array of numeric elements.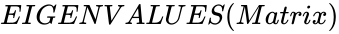 ,
,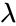 is a scalar which may be either real or complex.
is a scalar which may be either real or complex.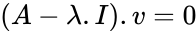 .
. .
.