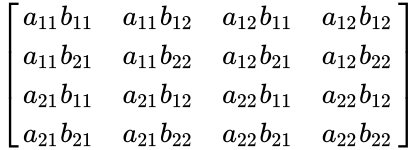Difference between revisions of "Manuals/calci/TENSORPRODUCT"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''TENSORPRODUCT (a,b) '''</div><br/> OR <div style="font-size:30px">'''MATRIXTENSORPRODUCT (a,b) '''</div><br/> *<math>a</math> and <math>b</math>...") |
|||
| Line 83: | Line 83: | ||
|28 || 72 || 43.2 || 17.5 || 45 ||27 ||10.5 || 27||16.200000000000003 | |28 || 72 || 43.2 || 17.5 || 45 ||27 ||10.5 || 27||16.200000000000003 | ||
|} | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=qp_zg_TD0qE|280|center|Tens or Product}} | ||
==See Also== | ==See Also== | ||
Revision as of 13:36, 2 May 2019
TENSORPRODUCT (a,b)
OR
MATRIXTENSORPRODUCT (a,b)
- and are any two matrices.
Description
- This function shows the Tensor product of the matrix.
- In , and are any two matrices.
- Here matrices and should be square matrix with same order.
- Tensor product is denoted by .
- Tensor product is different from general product.
- The Tensor product is defined by the product two vector spaces V and W is itself a Vector space.
- It is denoted by .
- A DYADIC product is the special case of the tensor product between two vectors of the same dimension.
- The tensor product of V and W is the vector space generated by the symbols , with and .
- The tensor product from the direct sum vector space, whose dimension is the sum of the dimensions of the two summands:
- Now consider any 2x2 matrices:
=
Examples
1. TENSORPRODUCT([[2,3],[1,0]],[[10,2],[6,-18]])
| 20 | 4 | 30 | 6 |
| 12 | -36 | 18 | -54 |
| 10 | 2 | 0 | 0 |
| 6 | -18 | 0 | 0 |
2. TENSORPRODUCT([[3,7.3,6],[10,11,-6],[8,5,3]],[[12,4,-5],[6,10,3],[3.5,9,5.4]])
| 36 | 12 | -15 | 87.6 | 29.2 | -36.5 | 72 | 24 | -30 |
| 18 | 30 | 9 | 43.8 | 73 | 21.9 | 36 | 60 | 18 |
| 10.5 | 27 | 16.200000000000003 | 25.55 | 65.7 | 39.42 | 21 | 54 | 32.400000000000006 |
| 120 | 40 | -50 | 132 | 44 | -55 | -72 | -24 | 30 |
| 60 | 100 | 30 | 66 | 110 | 33 | -36 | -60 | -18 |
| 35 | 90 | 54 | 38.5 | 99 | 59.400000000000006 | -21 | -54 | -32.400000000000006 |
| 96 | 32 | -40 | 60 | 20 | -25 | 36 | 12 | -15 |
| 48 | 80 | 24 | 30 | 50 | 15 | 18 | 30 | 9 |
| 28 | 72 | 43.2 | 17.5 | 45 | 27 | 10.5 | 27 | 16.200000000000003 |
 and
and 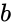 are any two matrices.
are any two matrices.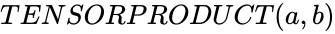 ,
,  .
.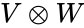 .
.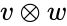 , with
, with 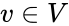 and
and 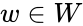 .
.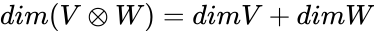
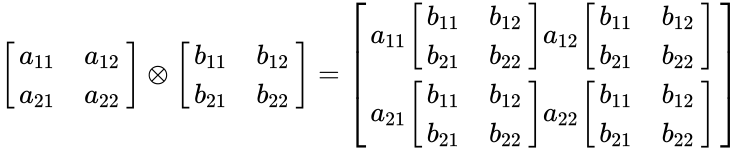 =
=