Difference between revisions of "Manuals/calci/BIRTHDAYPROBABILITY"
Jump to navigation
Jump to search
| Line 17: | Line 17: | ||
# BIRTHDAYPROBABILITY(20,432) = 0.3686145731391096 | # BIRTHDAYPROBABILITY(20,432) = 0.3686145731391096 | ||
# BIRTHDAYPROBABILITY(30.3,765) = 0.44899395029084743 | # BIRTHDAYPROBABILITY(30.3,765) = 0.44899395029084743 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=9G0w61pZPig|280|center|Birthday Probability}} | ||
==See Also== | ==See Also== | ||
Latest revision as of 12:39, 6 May 2019
BIRTHDAYPROBABILITY (NumberOfDuplicates,TotalNumberOfDays)
- is any real number.
- is the number of days.
Description
- This function shows the value of the Birthday probability.
- In , is the additional number of birthday.
- is the number of days.
- Birthday probability is the sum of the probability that an event will happen and the probability that the event won't happen is always 1.
- In a room of 75 there is a 99.9% chance of two people birthday matching.
- To work out the probability there is no two people will have the same birthday,the following rules to be followed to find the probability that two people will share a birthday:
P(two people share birthday) + P(no two people share birthday) = 1 P(two people share birthday) = 1 - P(no two people share birthday).
Examples
- BIRTHDAYPROBABILITY(3,30) = 0.1384203445582639
- BIRTHDAYPROBABILITY(20,432) = 0.3686145731391096
- BIRTHDAYPROBABILITY(30.3,765) = 0.44899395029084743
Related Videos
See Also
References
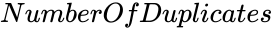 is any real number.
is any real number.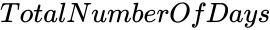 is the number of days.
is the number of days.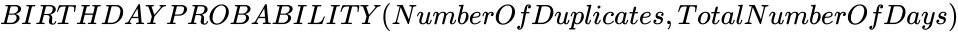 ,
,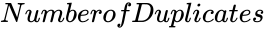 is the additional number of birthday.
is the additional number of birthday.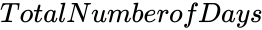 is the number of days.
is the number of days.