Difference between revisions of "Manuals/calci/VARPA"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> <font color="#484848"><font face="Arial, sans-serif"><font size="2">'''VARPA'''</font></font></font><font color="#4...") |
|||
| (11 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''VARPA()'''</div><br/> |
| + | *Parameters are set of numbers. | ||
| + | **VARPA(),calculates variance based on the entire population, including numbers, text, and logical values. | ||
| − | < | + | ==Description== |
| + | *This function gives the variance based on the entire population. | ||
| + | *Variance is a measure of dispersion obtained by taking the mean of the squared deviations of the observed values from their mean in a frequency distribution. | ||
| + | *i.e.,variance is a measure of how far each value in the data set is from the mean. | ||
| + | *It is denoted by <math> \sigma </math>. The square root of variance is called the standard deviation. | ||
| + | *In <math>VARPA()</math>, Parameters are numbers based on a population. Here First Parameter is required.From the Second Parameter are optional. | ||
| + | *To find the variance we can use the following formula: | ||
| + | <math>Variance= \frac{\sum (x_i-\bar{x})^2}{n-1}</math> | ||
| + | where <math> \bar{x}</math> is the sample mean of <math> x_i</math> and <math> n </math> is the sample size. | ||
| + | *Suppose <math>\sigma = 0</math> which is indicating all the values are identical. | ||
| + | *When <math>\sigma </math> is non-zero then it is always positive. | ||
| + | *This function is considering our given data is the entire population. | ||
| + | *Suppose it should consider the data as the sample of the population, we can use the [[Manuals/calci/VARA | VARA ]] function. | ||
| + | *The arguments can be either numbers or names, array,constants or references that contain numbers. | ||
| + | *Also we can give the text representations of numbers or logical values , like TRUE or FALSE, in a reference. | ||
| + | *Suppose the arguments containing TRUE which is evaluate as 1, and the arguments containing FALSE which is evaluate as 0. | ||
| + | *Suppose the array contains the empty cells and text values like that values are not considered. | ||
| + | *Suppose the function don't want to consider the logical values and text representations of numbers in a reference , we can use the [[Manuals/calci/VARP | VARP ]] function. | ||
| + | *This function will return the result as error when | ||
| + | 1. Any one of the argument is non-numeric. | ||
| + | 2. The arguments containing the error values or text that cannot be translated in to numbers. | ||
| − | + | ==Examples== | |
| − | + | {| class="wikitable" | |
| − | + | |+Spreadsheet | |
| − | + | |- | |
| − | + | ! !! A !! B !! C !! D!! E !! F | |
| − | + | |- | |
| − | + | ! 1 | |
| − | + | | 40 || 45 || 60 || 24 || 72 || 81 | |
| − | + | |- | |
| − | + | ! 2 | |
| − | + | | 10.21 || 11.65 || 17.81 || 15.02 || 18.18 || 27.41 | |
| − | + | |} | |
| − | + | #=VARPA(A1:F1) = 377.555555556 | |
| − | + | #=VARPA(A1:F2) = 31.4284222222 | |
| − | + | #=VARPA(12,23,34,45,true) = 242 | |
| − | + | #=VARPA(12,23,34,45,FALSE) = 250.96000000000004 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Related Videos== | |
| − | + | {{#ev:youtube|2evEY6MTxZQ|280|center|Sample Variance}} | |
| − | + | ==See Also== | |
| + | *[[Manuals/calci/DVAR | DVAR ]] | ||
| + | *[[Manuals/calci/DVARP | DVARP ]] | ||
| + | *[[Manuals/calci/VARP | VARP ]] | ||
| + | *[[Manuals/calci/VAR | VAR]] | ||
| − | + | ==References== | |
| + | *[http://en.wikipedia.org/wiki/Variance Variance] | ||
| − | |||
| − | |||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *[[ Z3 | Z3 home ]] | |
| − | |||
| − | |||
| − | |||
Latest revision as of 00:22, 1 July 2019
VARPA()
- Parameters are set of numbers.
- VARPA(),calculates variance based on the entire population, including numbers, text, and logical values.
Description
- This function gives the variance based on the entire population.
- Variance is a measure of dispersion obtained by taking the mean of the squared deviations of the observed values from their mean in a frequency distribution.
- i.e.,variance is a measure of how far each value in the data set is from the mean.
- It is denoted by . The square root of variance is called the standard deviation.
- In , Parameters are numbers based on a population. Here First Parameter is required.From the Second Parameter are optional.
- To find the variance we can use the following formula:
where is the sample mean of and is the sample size.
- Suppose which is indicating all the values are identical.
- When is non-zero then it is always positive.
- This function is considering our given data is the entire population.
- Suppose it should consider the data as the sample of the population, we can use the VARA function.
- The arguments can be either numbers or names, array,constants or references that contain numbers.
- Also we can give the text representations of numbers or logical values , like TRUE or FALSE, in a reference.
- Suppose the arguments containing TRUE which is evaluate as 1, and the arguments containing FALSE which is evaluate as 0.
- Suppose the array contains the empty cells and text values like that values are not considered.
- Suppose the function don't want to consider the logical values and text representations of numbers in a reference , we can use the VARP function.
- This function will return the result as error when
1. Any one of the argument is non-numeric.
2. The arguments containing the error values or text that cannot be translated in to numbers.
Examples
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | 40 | 45 | 60 | 24 | 72 | 81 |
| 2 | 10.21 | 11.65 | 17.81 | 15.02 | 18.18 | 27.41 |
- =VARPA(A1:F1) = 377.555555556
- =VARPA(A1:F2) = 31.4284222222
- =VARPA(12,23,34,45,true) = 242
- =VARPA(12,23,34,45,FALSE) = 250.96000000000004
Related Videos
See Also
References
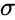 . The square root of variance is called the standard deviation.
. The square root of variance is called the standard deviation.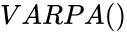 , Parameters are numbers based on a population. Here First Parameter is required.From the Second Parameter are optional.
, Parameters are numbers based on a population. Here First Parameter is required.From the Second Parameter are optional.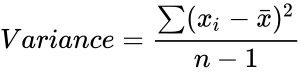 where
where 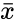 is the sample mean of
is the sample mean of 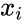 and
and  is the sample size.
is the sample size.
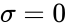 which is indicating all the values are identical.
which is indicating all the values are identical.