Difference between revisions of "Manuals/calci/NORMSINV"
Jump to navigation
Jump to search
| (6 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''NORMSINV( | + | <div style="font-size:30px">'''NORMSINV (Probability)'''</div><br/> |
| − | *<math> | + | *<math>Probability</math> is the value of the Probability. |
| + | ** NORMSINV(),returns the inverse of the standard normal cumulative distribution. | ||
==Description== | ==Description== | ||
*This function gives the inverse of the Standard Normal Cumulative Distribution. | *This function gives the inverse of the Standard Normal Cumulative Distribution. | ||
*In Normal Distribution formula, when the Mean is zero and the Standard Deviation is 1 then it is called Standard Normal Distribution. | *In Normal Distribution formula, when the Mean is zero and the Standard Deviation is 1 then it is called Standard Normal Distribution. | ||
| − | *If <math> NORMSDIST( | + | *If <math> NORMSDIST (Number,Accuracy)=Probability</math>, then <math>NORMSINV (Probability)=Number</math>. |
| − | *<math>NORMSINV</math> using the iterating method to find the value of <math> | + | *<math>NORMSINV</math> using the iterating method to find the value of <math>Number</math>. |
*Suppose the iteration has not converged after 100 searches, then the function gives the error result. | *Suppose the iteration has not converged after 100 searches, then the function gives the error result. | ||
| − | *In <math>NORMSINV( | + | *In <math>NORMSINV (Probability)</math>, where <math>Probability</math> is the probability value of the Standard Normal Cumulative Distribution. |
*This function will return the result as error when | *This function will return the result as error when | ||
| − | 1. | + | 1.Probability is non-numeric. |
| − | 2. | + | 2.Probability<0 or Probability>1. |
==Examples== | ==Examples== | ||
#=NORMSINV(0.9999975333) = 4.567600 | #=NORMSINV(0.9999975333) = 4.567600 | ||
#=NORMSINV(0.00241) = -2.818823592 | #=NORMSINV(0.00241) = -2.818823592 | ||
| − | #=NORMSINV(1) = | + | #=NORMSINV(1) = #N/A (PROBABILITY >0 (OR) PROBABILITY < 1) |
#=NORMSINV(0.00001) = -4.264890794 | #=NORMSINV(0.00001) = -4.264890794 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|F2rKy2cI8Ss|280|center|NORMSINV}} | ||
==See Also== | ==See Also== | ||
| Line 26: | Line 31: | ||
==References== | ==References== | ||
[http://en.wikipedia.org/wiki/Normal_distribution Normal Distribution] | [http://en.wikipedia.org/wiki/Normal_distribution Normal Distribution] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 09:29, 2 June 2020
NORMSINV (Probability)
- is the value of the Probability.
- NORMSINV(),returns the inverse of the standard normal cumulative distribution.
Description
- This function gives the inverse of the Standard Normal Cumulative Distribution.
- In Normal Distribution formula, when the Mean is zero and the Standard Deviation is 1 then it is called Standard Normal Distribution.
- If , then .
- using the iterating method to find the value of .
- Suppose the iteration has not converged after 100 searches, then the function gives the error result.
- In , where is the probability value of the Standard Normal Cumulative Distribution.
- This function will return the result as error when
1.Probability is non-numeric. 2.Probability<0 or Probability>1.
Examples
- =NORMSINV(0.9999975333) = 4.567600
- =NORMSINV(0.00241) = -2.818823592
- =NORMSINV(1) = #N/A (PROBABILITY >0 (OR) PROBABILITY < 1)
- =NORMSINV(0.00001) = -4.264890794
Related Videos
See Also
References
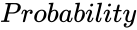 is the value of the Probability.
is the value of the Probability.
 , then
, then 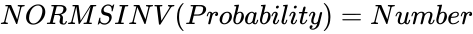 .
.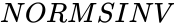 using the iterating method to find the value of
using the iterating method to find the value of 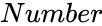 .
.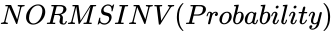 , where
, where