Difference between revisions of "Manuals/calci/PASCALTRIANGLE"
Jump to navigation
Jump to search
| (14 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''PASCALTRIANGLE( | + | <div style="font-size:30px">'''PASCALTRIANGLE (Levels)'''</div><br/> |
| − | *<math> | + | *<math>Levels</math> is the level number of the Pascal Triangle. |
| + | **PASCALTRIANGLE(), is a triangle of numbers in which a row represents the coefficients of the binomial series. | ||
==Description== | ==Description== | ||
*This function gives the Coefficients of the Pascal triangle. | *This function gives the Coefficients of the Pascal triangle. | ||
| − | *In <math>PASCALTRIANGLE( | + | *In <math>PASCALTRIANGLE(Levels)</math> , <math>Levels</math> is the level number of the Pascal triangle. |
*Pascal triangle is the arrangement of numbers of the Binomial coefficients in a triangular shape. | *Pascal triangle is the arrangement of numbers of the Binomial coefficients in a triangular shape. | ||
| − | *It is started with the number 1 at the top in the 1st row. | + | *It is started with the number <math>1</math> at the top in the 1st row. |
*Then from the 2nd row each number in the triangle is the sum of the two directly above it. | *Then from the 2nd row each number in the triangle is the sum of the two directly above it. | ||
| − | *The construction is related to the | + | *The construction is related to the Binomial Coefficients by Pascal's rule is : |
| − | <math>(x+y)^n=\sum_{k=0}^n \binom{n}{k}x^{n-k} .y^k </math>. | + | <math>(x+y)^n=\sum_{k=0}^n \binom{n}{k}x^{n-k} .y^k </math>. |
| − | *This function will return the result as error when | + | where <math> \dbinom{n}{k}</math> is the binomial coefficient. |
| + | *This function will return the result as error when <math> r \le 0</math>. | ||
==Examples== | ==Examples== | ||
| − | *1.PASCALTRIANGLE(1) | + | *1.=PASCALTRIANGLE(1) |
| − | *2.PASCALTRIANGLE(2) | + | 1 |
| + | *2.=PASCALTRIANGLE(2) | ||
| + | 1 | ||
1 1 | 1 1 | ||
| − | *3.PASCALTRIANGLE(3) | + | *3.=PASCALTRIANGLE(3) |
| + | 1 | ||
1 1 | 1 1 | ||
1 2 1 | 1 2 1 | ||
| − | *4.PASCALTRIANGLE(0)=NULL | + | *4.=PASCALTRIANGLE(0) = NULL |
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v9Evg2tBdRk|280|center|PASCAL'S TRIANGLE}} | ||
==See Also== | ==See Also== | ||
| + | *[[Manuals/calci/BINOMDIST | BINOMDIST ]] | ||
| + | *[[Manuals/calci/Pascal Triangle Fun | Pascal Triangle Fun Facts ]] | ||
==References== | ==References== | ||
* [http://www.mathsisfun.com/pascals-triangle.html Pascal's Triangle ] | * [http://www.mathsisfun.com/pascals-triangle.html Pascal's Triangle ] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *[[ Z3 | Z3 home ]] | |
| − | |||
Latest revision as of 16:34, 6 August 2020
PASCALTRIANGLE (Levels)
- is the level number of the Pascal Triangle.
- PASCALTRIANGLE(), is a triangle of numbers in which a row represents the coefficients of the binomial series.
Description
- This function gives the Coefficients of the Pascal triangle.
- In , is the level number of the Pascal triangle.
- Pascal triangle is the arrangement of numbers of the Binomial coefficients in a triangular shape.
- It is started with the number at the top in the 1st row.
- Then from the 2nd row each number in the triangle is the sum of the two directly above it.
- The construction is related to the Binomial Coefficients by Pascal's rule is :
. where is the binomial coefficient.
- This function will return the result as error when .
Examples
- 1.=PASCALTRIANGLE(1)
1
- 2.=PASCALTRIANGLE(2)
1
1 1
- 3.=PASCALTRIANGLE(3)
1
1 1
1 2 1
- 4.=PASCALTRIANGLE(0) = NULL
Related Videos
See Also
References
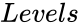 is the level number of the Pascal Triangle.
is the level number of the Pascal Triangle.
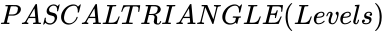 ,
,  at the top in the 1st row.
at the top in the 1st row.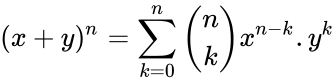 .
where
.
where 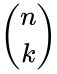 is the binomial coefficient.
is the binomial coefficient.
 .
.