Difference between revisions of "Manuals/calci/GAMMALN"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> <font size="3"><font face="Times New Roman">'''GAMMALN'''('''x''')</font></font> <font size="3"><font face="Times ...") |
|||
| (15 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''GAMMALN(x)'''</div><br/> |
| + | *<math>x</math> is the number. | ||
| + | **GAMMALN(), returns the natural logarithm of the Gamma Function. | ||
| − | < | + | ==Description== |
| + | *This function gives the natural logarithm of the absolute value of the Gamma Function. | ||
| + | *The functions Digamma and Trigamma are the first and second derivatives of the logarithm of the Gamma Function. | ||
| + | *This is often called the Polygamma function. | ||
| + | *Gamma, Lgamma, Digamma and Trigamma functions are internal generic primitive functions. | ||
| + | *Normally the number <math>e to the power {GAMMALN(x)}</math>, where <math>x</math> is an integer, is same as <math>(x-1)!</math>. | ||
| + | :<math>GAMMALN=LN( \Gamma(x)</math>, | ||
| + | where | ||
| + | : <math> \Gamma(x) = \int\limits_{0}^{\infty} t^{x-1} e^{-t} dt</math> | ||
| + | it is for all complex numbers except the negative integers and zero. | ||
| + | *This function will give the result as error when | ||
| + | <math>x</math> is non-numeric and <math>x \le 0</math>. | ||
| − | + | ==Examples== | |
| + | #GAMMALN(6) = 4.787491744416229 | ||
| + | #GAMMALN(42) = 114.03421178146174 | ||
| + | #GAMMALN(1) = 0.00018319639111644828(calci) | ||
| + | #GAMMALN(-10) = #N/A (X <= 0) | ||
| − | + | ==Related Videos== | |
| − | |||
| − | |||
| − | + | {{#ev:youtube|SAMTXAAKeug|280|center|GAMMA Distribution}} | |
| − | + | ==See Also== | |
| − | + | *[[Manuals/calci/GAMMADIST | GAMMADIST ]] | |
| − | + | *[[Manuals/calci/FACT | FACT]] | |
| + | *[[Manuals/calci/LN | LN]] | ||
| − | + | ==References== | |
| + | [http://en.wikipedia.org/wiki/Gamma_distribution Gamma Distribution]* | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| − | + | *[[ Z3 | Z3 home ]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 03:58, 12 August 2020
GAMMALN(x)
- is the number.
- GAMMALN(), returns the natural logarithm of the Gamma Function.
Description
- This function gives the natural logarithm of the absolute value of the Gamma Function.
- The functions Digamma and Trigamma are the first and second derivatives of the logarithm of the Gamma Function.
- This is often called the Polygamma function.
- Gamma, Lgamma, Digamma and Trigamma functions are internal generic primitive functions.
- Normally the number , where is an integer, is same as .
- ,
where
it is for all complex numbers except the negative integers and zero.
- This function will give the result as error when
is non-numeric and .
Examples
- GAMMALN(6) = 4.787491744416229
- GAMMALN(42) = 114.03421178146174
- GAMMALN(1) = 0.00018319639111644828(calci)
- GAMMALN(-10) = #N/A (X <= 0)
Related Videos
See Also
References
 is the number.
is the number.
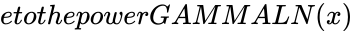 , where
, where 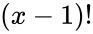 .
.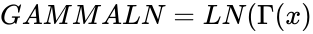 ,
,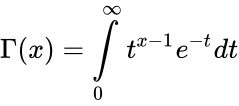
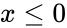 .
.