Difference between revisions of "Manuals/calci/CRITBINOM"
Jump to navigation
Jump to search
| (12 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''CRITBINOM( | + | <div style="font-size:30px">'''CRITBINOM(trials,probabilitys,alpha,accuracy)'''</div><br/> |
| − | *<math> | + | *<math>trials</math> is the number of independent trials. |
| − | *<math> | + | *<math>probabilitys</math> is the probability of success in one trial. |
*<math>alpha</math> is the criterion value. | *<math>alpha</math> is the criterion value. | ||
| + | *<math>accuracy</math> gives accurate value of the solution. | ||
| + | **CRITBINOM(), returns the smallest value for which the cumulative binomial distribution is less than or equal to a criterion value. | ||
| + | |||
==Description== | ==Description== | ||
| − | * | + | *The smallest value in Cumulative Binomial Distribution probability result is the Critbinom. |
*This function is the inverse of the Cumulative Binomial Distribution. | *This function is the inverse of the Cumulative Binomial Distribution. | ||
*For example, the Critbinom function could be used to find the smallest number of through the dice for which there is a 40% chance of at least 10 six's. | *For example, the Critbinom function could be used to find the smallest number of through the dice for which there is a 40% chance of at least 10 six's. | ||
| − | *In CRITBINOM( | + | *In CRITBINOM(trials,probabilitys,alpha,accuracy), <math>trials</math> is the number of independent trials that are to be done (if <math>trials</math> value is in decimal then it is converted to an integer). |
| + | *<math>probabilitys</math> is the probability of success in one trial and <math>alpha</math> is the criterion value of the Cumulative Binomial Distribution (must be between 0 and 1). | ||
| + | *<math>accuracy</math> gives accurate value of the solution. | ||
*This function gives the result as error when | *This function gives the result as error when | ||
1.Any one of the argument is non-numeric. | 1.Any one of the argument is non-numeric. | ||
| − | 2.<math> | + | 2.<math>trials<0</math>,or <math>probabilitys<0</math> or <math>probabilitys>1</math> |
| − | 3.<math>alpha<0</math> or <math>alpha>1</math> | + | 3.<math>alpha<0</math> or <math>alpha>1</math>. |
| + | |||
| + | ==ZOS== | ||
| + | *The syntax is to calculate CRITBINOM in ZOS is <math>CRITBINOM(trials,probabilitys,alpha,accuracy)</math>. | ||
| + | **<math>trials</math> is the number of independent trials. | ||
| + | **<math>probabilitys</math> is the probability of success in one trial. | ||
| + | **<math>alpha</math> is the criterion value. | ||
| + | **<math>accuracy</math> gives accurate value of the solution. | ||
| + | *For e.g.,CRITBINOM(5..8,0.5,0.4,0.02) | ||
| + | {{#ev:youtube|VqXa3JGsSvY|280|center|CRITBINOM }} | ||
==Examples== | ==Examples== | ||
| Line 18: | Line 32: | ||
#CRITBINOM(8,0.1,0.25) = 1 | #CRITBINOM(8,0.1,0.25) = 1 | ||
#CRITBINOM(20,0.75,0.65) = 16 | #CRITBINOM(20,0.75,0.65) = 16 | ||
| − | #CRITBINOM(20,1,1.5) = | + | #CRITBINOM(20,1,1.5) = #N/A (ALPHA IN BETWEEN 0 AND 1 REQUIRED) |
#CRITBINOM(9.5,0.4,0.35) = 3 | #CRITBINOM(9.5,0.4,0.35) = 3 | ||
| − | #CRITBINOM(12,-0.25,0.3) = | + | #CRITBINOM(12,-0.25,0.3) = #N/A (PROBABILITY IN BETWEEN 0 AND 1 REQUIRED) |
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|L6YX3ug1znM|280|center|Cumulative Probability}} | ||
==See Also== | ==See Also== | ||
| Line 28: | Line 46: | ||
*[[Manuals/calci/FACT | FACT ]] | *[[Manuals/calci/FACT | FACT ]] | ||
==References== | ==References== | ||
| − | [http://en.wikipedia.org/wiki/ | + | [http://en.wikipedia.org/wiki/Binomial_distribution Binomial Distribution] |
| + | |||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 03:32, 25 August 2020
CRITBINOM(trials,probabilitys,alpha,accuracy)
- is the number of independent trials.
- is the probability of success in one trial.
- is the criterion value.
- gives accurate value of the solution.
- CRITBINOM(), returns the smallest value for which the cumulative binomial distribution is less than or equal to a criterion value.
Description
- The smallest value in Cumulative Binomial Distribution probability result is the Critbinom.
- This function is the inverse of the Cumulative Binomial Distribution.
- For example, the Critbinom function could be used to find the smallest number of through the dice for which there is a 40% chance of at least 10 six's.
- In CRITBINOM(trials,probabilitys,alpha,accuracy), is the number of independent trials that are to be done (if value is in decimal then it is converted to an integer).
- is the probability of success in one trial and is the criterion value of the Cumulative Binomial Distribution (must be between 0 and 1).
- gives accurate value of the solution.
- This function gives the result as error when
1.Any one of the argument is non-numeric. 2.,or or 3. or .
ZOS
- The syntax is to calculate CRITBINOM in ZOS is .
- is the number of independent trials.
- is the probability of success in one trial.
- is the criterion value.
- gives accurate value of the solution.
- For e.g.,CRITBINOM(5..8,0.5,0.4,0.02)
Examples
- CRITBINOM(5,0.6,0.4) = 3
- CRITBINOM(8,0.1,0.25) = 1
- CRITBINOM(20,0.75,0.65) = 16
- CRITBINOM(20,1,1.5) = #N/A (ALPHA IN BETWEEN 0 AND 1 REQUIRED)
- CRITBINOM(9.5,0.4,0.35) = 3
- CRITBINOM(12,-0.25,0.3) = #N/A (PROBABILITY IN BETWEEN 0 AND 1 REQUIRED)
Related Videos
See Also
References
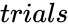 is the number of independent trials.
is the number of independent trials.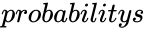 is the probability of success in one trial.
is the probability of success in one trial.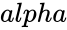 is the criterion value.
is the criterion value.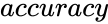 gives accurate value of the solution.
gives accurate value of the solution.
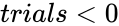 ,or
,or 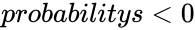 or
or 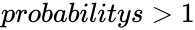 3.
3.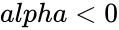 or
or 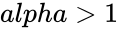 .
.
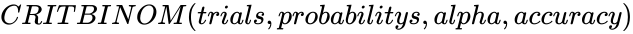 .
.