Difference between revisions of "Manuals/calci/BESSELJ"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> <font color="#484848"><font face="Arial, sans-serif"><font size="2">'''BESSELJ'''</font></font></font><font color="#484...") |
|||
| (20 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''BESSELJ(x,n)'''</div><br/> |
| + | *<math>x</math> is the value to evaluate the function | ||
| + | *<math>n</math> is the order of the Bessel function and is an integer. | ||
| + | **BESSELJ(), returns the modified Bessel Function Jn(x). | ||
| − | < | + | ==Description== |
| + | *This function gives the value of the modified Bessel function. | ||
| + | *Bessel functions is also called Cylinder Functions because they appear in the solution to Laplace's equation in cylindrical coordinates. | ||
| + | *Bessel's Differential Equation is defined as: <math>x^2\frac{d^2 y}{dx^2} + x\frac{dy}{dx} + (x^2 - \alpha^2)y =0</math> | ||
| + | where <math>\alpha</math> is the arbitrary Complex Number. | ||
| + | *But in most of the cases <math>\alpha</math> is the non-negative real number. | ||
| + | *The solutions of this equation are called Bessel Functions of order n. | ||
| + | *Bessel functions of the first kind, denoted as <math>J_n(x)</math> | ||
| + | *The Bessel function of the first kind of order can be expressed as: | ||
| + | <math>J_n(x)=\sum_{k=0}^\infty \frac{(-1)^k*(\frac{x}{2})^{n+2k} }{k!\Gamma(n+k+1)}</math> | ||
| + | *where <math>\Gamma(n+k+1)=(n+k)!</math> or | ||
| + | *<math>\int\limits_{0}^{\infty} x^{n+k}*e^{-x} dx</math> is the Gamma Function. | ||
| + | *This function will give result as error when | ||
| + | 1. <math>x</math> or <math>n</math> is non numeric | ||
| + | 2. <math>n < 0</math>, because <math>n</math> is the order of the function. | ||
| − | + | ==ZOS== | |
| − | + | *The syntax is to calculate BESSELJ in ZOS is <math>BESSELJ(x,n)</math>. | |
| − | + | **<math>x</math> is the value to evaluate the function | |
| − | + | **<math>n</math> is the order of the Bessel function and is an integer. | |
| − | + | *For e.g.,BESSELJ(0.789..0.901..0.025,5) | |
| − | + | ==Examples== | |
| − | |||
| − | |||
| − | + | #BESSELJ(2,3) = 0.12894324997562717 | |
| + | #BESSELJ(7,2) = -0.3014172238218034 | ||
| + | #BESSELJ(5,1) = -0.3275791385663632 | ||
| − | + | ==Related Videos== | |
| − | + | {{#ev:youtube|__fdGscBZjI|280|center|BESSEL Equation}} | |
| − | + | ==See Also== | |
| + | *[[Manuals/calci/BESSELI | BESSELI ]] | ||
| + | *[[Manuals/calci/BESSELK | BESSELK ]] | ||
| + | *[[Manuals/calci/BESSELY | BESSELY ]] | ||
| − | + | ==References== | |
| + | [http://en.wikipedia.org/wiki/Bessel_function Bessel Function] | ||
| − | |||
| − | |||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| − | + | *[[ Z3 | Z3 home ]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 08:02, 29 September 2021
BESSELJ(x,n)
- is the value to evaluate the function
- is the order of the Bessel function and is an integer.
- BESSELJ(), returns the modified Bessel Function Jn(x).
Description
- This function gives the value of the modified Bessel function.
- Bessel functions is also called Cylinder Functions because they appear in the solution to Laplace's equation in cylindrical coordinates.
- Bessel's Differential Equation is defined as:
where is the arbitrary Complex Number.
- But in most of the cases is the non-negative real number.
- The solutions of this equation are called Bessel Functions of order n.
- Bessel functions of the first kind, denoted as
- The Bessel function of the first kind of order can be expressed as:
- where or
- is the Gamma Function.
- This function will give result as error when
1. or is non numeric 2. , because is the order of the function.
ZOS
- The syntax is to calculate BESSELJ in ZOS is .
- is the value to evaluate the function
- is the order of the Bessel function and is an integer.
- For e.g.,BESSELJ(0.789..0.901..0.025,5)
Examples
- BESSELJ(2,3) = 0.12894324997562717
- BESSELJ(7,2) = -0.3014172238218034
- BESSELJ(5,1) = -0.3275791385663632
Related Videos
See Also
References
 is the value to evaluate the function
is the value to evaluate the function is the order of the Bessel function and is an integer.
is the order of the Bessel function and is an integer.
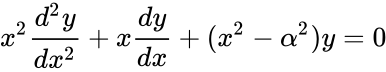
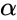 is the arbitrary Complex Number.
is the arbitrary Complex Number.
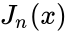
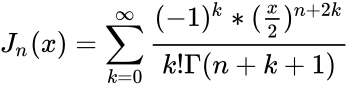
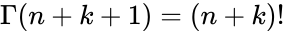 or
or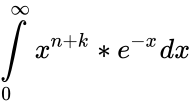 is the Gamma Function.
is the Gamma Function.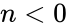 , because
, because 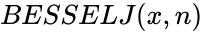 .
.