Difference between revisions of "Manuals/calci/BESSELY"
Jump to navigation
Jump to search
| (13 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''BESSELY(x,n)'''</div><br/> | <div style="font-size:30px">'''BESSELY(x,n)'''</div><br/> | ||
| − | * | + | *<math>x</math> is the value at which to evaluate the function |
*<math>n</math> is the integer which is the order of the Bessel Function | *<math>n</math> is the integer which is the order of the Bessel Function | ||
| + | **BESSELY(), returns the Bessel Function Yn(x) | ||
==Description== | ==Description== | ||
*This function gives the value of the modified Bessel function. | *This function gives the value of the modified Bessel function. | ||
| Line 10: | Line 11: | ||
*The solutions of this equation are called Bessel Functions of order <math>n</math>. | *The solutions of this equation are called Bessel Functions of order <math>n</math>. | ||
*The Bessel function of the second kind <math>Yn(x)</math> and sometimes it is called Weber Function or the Neumann Function.. | *The Bessel function of the second kind <math>Yn(x)</math> and sometimes it is called Weber Function or the Neumann Function.. | ||
| − | *The Bessel function of the 2nd kind of order can be expressed as: <math>Yn(x)= \lim_{p \to n}\frac{J_p(x)Cos(p\pi)- | + | *The Bessel function of the 2nd kind of order can be expressed as: <math>Yn(x)= \lim_{p \to n}\frac{J_p(x)Cos(p\pi)- J_{-p}(x)}{Sin(p\pi)}</math> |
| − | *where Jn(x) is the Bessel functions of the first kind. | + | *where <math>Jn(x)</math> is the Bessel functions of the first kind. |
| − | *This function will give the result as error when 1.x or n is non | + | *This function will give the result as error when: |
| + | 1. <math>x</math> or <math>n</math> is non numeric | ||
| + | 2. <math>n<0</math>, because <math>n</math> is the order of the function. | ||
| + | |||
| + | ==ZOS== | ||
| + | *The syntax is to calculate BESSELY in ZOS is <math>BESSELY(x,n)</math>. | ||
| + | **<math>x</math> is the value at which to evaluate the function | ||
| + | **<math>n</math> is the integer which is the order of the Bessel Function | ||
==Examples== | ==Examples== | ||
| − | #BESSELY(2,3)=-1. | + | #=BESSELY(2,3) = -1.1277837651220644 |
| − | #BESSELY(0.7,4)=-132. | + | #=BESSELY(0.7,4)= -132.6340573047033 |
| − | #BESSELY(9,1)=0. | + | #=BESSELY(9,1) = 0.10431457495919716 |
| − | #BESSELY(2,-1)= | + | #=BESSELY(2,-1) = #N/A (ORDER OF FUNCTION < 0) |
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|__fdGscBZjI|280|center|BESSEL Equation}} | ||
==See Also== | ==See Also== | ||
| Line 27: | Line 39: | ||
==References== | ==References== | ||
| − | [http://en.wikipedia.org/wiki/ | + | [http://en.wikipedia.org/wiki/Bessel_function Bessel Function] |
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 07:07, 29 September 2021
BESSELY(x,n)
- is the value at which to evaluate the function
- is the integer which is the order of the Bessel Function
- BESSELY(), returns the Bessel Function Yn(x)
Description
- This function gives the value of the modified Bessel function.
- Bessel functions is also called Cylinder Functions because they appear in the solution to Laplace's equation in cylindrical coordinates.
- Bessel's Differential Equation is defined as:
where is the arbitrary complex number.
- But in most of the cases is the non-negative real number.
- The solutions of this equation are called Bessel Functions of order .
- The Bessel function of the second kind and sometimes it is called Weber Function or the Neumann Function..
- The Bessel function of the 2nd kind of order can be expressed as:
- where is the Bessel functions of the first kind.
- This function will give the result as error when:
1. or is non numeric 2. , because is the order of the function.
ZOS
- The syntax is to calculate BESSELY in ZOS is .
- is the value at which to evaluate the function
- is the integer which is the order of the Bessel Function
Examples
- =BESSELY(2,3) = -1.1277837651220644
- =BESSELY(0.7,4)= -132.6340573047033
- =BESSELY(9,1) = 0.10431457495919716
- =BESSELY(2,-1) = #N/A (ORDER OF FUNCTION < 0)
Related Videos
See Also
References
 is the value at which to evaluate the function
is the value at which to evaluate the function is the integer which is the order of the Bessel Function
is the integer which is the order of the Bessel Function
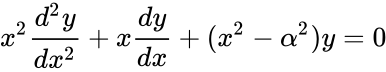
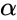 is the arbitrary complex number.
is the arbitrary complex number.
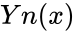 and sometimes it is called Weber Function or the Neumann Function..
and sometimes it is called Weber Function or the Neumann Function..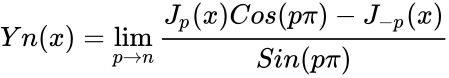
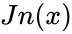 is the Bessel functions of the first kind.
is the Bessel functions of the first kind.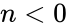 , because
, because 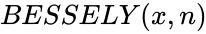 .
.