Difference between revisions of "Manuals/calci/FOURTHROOT"
Jump to navigation
Jump to search
| (3 intermediate revisions by 2 users not shown) | |||
| Line 15: | Line 15: | ||
#FOURTHROOT(7612) = 9.340598291584374 | #FOURTHROOT(7612) = 9.340598291584374 | ||
#FOURTHROOT(-625) = 0-ⅈ5 | #FOURTHROOT(-625) = 0-ⅈ5 | ||
| + | #√√64 = 2.8284271247461903 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=OHJ-UXFhU64|280|center|Fourth Root}} | ||
==See Also== | ==See Also== | ||
| − | + | *[[Manuals/calci/CUBEROOT | CUBEROOT ]] | |
*[[Manuals/calci/NTHROOT | NTHROOT ]] | *[[Manuals/calci/NTHROOT | NTHROOT ]] | ||
*[[Z_API_Functions | List of Main Z Functions]] | *[[Z_API_Functions | List of Main Z Functions]] | ||
| Line 24: | Line 29: | ||
==References== | ==References== | ||
*[https://en.wikipedia.org/wiki/Nth_root Nth root] | *[https://en.wikipedia.org/wiki/Nth_root Nth root] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 03:57, 28 February 2022
FOURTHROOT (Number)
- is any real number.
Description
- This function shows the Fourth root of a given number.
- The fourth root of a number is the number that would have to be multiplied by itself 4 times to get the original number.
- For example, the fourth root of 81 is 3 as 3 x 3 x 3 x 3 is 81.
- Generally Second root is called Square root and Third root is called Cube root.
- These roots are easy to calculate by hand but even for perfect fourth root numbers, fourth root can be difficult to calculate by hand.
- So we can use this function to calculate the fourth root of the number with in a second.
Examples
- FOURTHROOT(16) = 2
- FOURTHROOT(234256) =22
- FOURTHROOT(7612) = 9.340598291584374
- FOURTHROOT(-625) = 0-ⅈ5
- √√64 = 2.8284271247461903
Related Videos
See Also
References
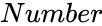 is any real number.
is any real number.