Difference between revisions of "Manuals/calci/ASINH"
| (7 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''ASINH( | + | <div style="font-size:30px">'''ASINH(Number)'''</div><br/> |
| − | * | + | * <math>Number</math> is any real number. |
| + | **ASINH() returns the inverse hyperbolic sine of a number. | ||
| + | |||
==Description== | ==Description== | ||
*This function gives the Inverse Hyperbolic Sine of a number. | *This function gives the Inverse Hyperbolic Sine of a number. | ||
*Here 'z' is any real number. | *Here 'z' is any real number. | ||
| − | *Inverse Hyperbolic Sine of a number is defined as <math> Asinh(z) = | + | *Inverse Hyperbolic Sine of a number is defined as <math> Asinh(z) = \log_e(z +\sqrt{z^2 + 1})</math> |
| − | *Also | + | *Also <math>ASinh(Sinh(z))=z</math> |
*ASINH(-z) = -ASINH(z) | *ASINH(-z) = -ASINH(z) | ||
| Line 17: | Line 19: | ||
|- class="even" | |- class="even" | ||
|'''ASINH(z)''' | |'''ASINH(z)''' | ||
| − | |'''Value | + | |'''Value''' |
|- class="odd" | |- class="odd" | ||
| Line 31: | Line 33: | ||
| -5.192987713658952 | | -5.192987713658952 | ||
|} | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|AQT2uHlyjEs|280|center|Inverse Hyperbolic SIN}} | ||
==See Also== | ==See Also== | ||
| Line 43: | Line 49: | ||
*[http://en.wikipedia.org/wiki/Trigonometric_functions List of Trigonometric Functions] | *[http://en.wikipedia.org/wiki/Trigonometric_functions List of Trigonometric Functions] | ||
*[http://en.wikipedia.org/wiki/Hyperbolic_function Hyperbolic Function] | *[http://en.wikipedia.org/wiki/Hyperbolic_function Hyperbolic Function] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 17:31, 13 August 2018
ASINH(Number)
- is any real number.
- ASINH() returns the inverse hyperbolic sine of a number.
Description
- This function gives the Inverse Hyperbolic Sine of a number.
- Here 'z' is any real number.
- Inverse Hyperbolic Sine of a number is defined as
- Also
- ASINH(-z) = -ASINH(z)
Examples
ASINH(z)
- z is any real number.
| ASINH(z) | Value |
| ASINH(2) | 1.44363547517881 |
| ASINH(45) | 4.499933104264103 |
| ASINH(-90) | -5.192987713658952 |
Related Videos
See Also
References
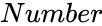 is any real number.
is any real number.