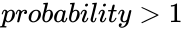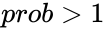Difference between revisions of "Manuals/calci/GAMMAINV"
Jump to navigation
Jump to search
| (6 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''GAMMAINV( | + | <div style="font-size:30px">'''GAMMAINV (probability,alpha,beta,accuracy,somenumberofiterations)'''</div><br/> |
| − | *<math> | + | *<math>probability</math> is the probability value associated with gamma distribution |
| − | *<math>alpha(\alpha)</math> & <math>beta(\beta)</math> are the values of the shape and rate parameters | + | *<math>alpha(\alpha)</math> & <math>beta(\beta)</math> are the values of the shape and rate parameters. |
| + | *<math> accuracy </math> gives accurate value of the solution. | ||
| + | *<math> somenumberofiterations </math> is any positive integer. | ||
| + | **GAMMAINV(),returns the inverse of the gamma cumulative distribution. | ||
| + | |||
==Description== | ==Description== | ||
*This function gives the inverse value of Cumulative Gamma Probability Distribution. | *This function gives the inverse value of Cumulative Gamma Probability Distribution. | ||
*This distribution is the Continuous Probability Distribution on the positive real line and it is of the reciprocal of a variable distributed according to the gamma distribution with two parameters <math>\alpha</math> & <math>\beta</math>. | *This distribution is the Continuous Probability Distribution on the positive real line and it is of the reciprocal of a variable distributed according to the gamma distribution with two parameters <math>\alpha</math> & <math>\beta</math>. | ||
*It is used in Bayesian statistics. | *It is used in Bayesian statistics. | ||
| − | *In <math>GAMMAINV( | + | *In <math>GAMMAINV (probability,alpha,beta,accuracy,somenumberofiterations)</math> , <math> probability </math> is the probability value associated with Gamma Distribution,<math>alpha</math> is called shape parameter and <math>beta</math> is the rate parameter of the distribution. |
| − | *If <math>GAMMADIST(x,alpha,beta, | + | *If <math>GAMMADIST (x,alpha,beta,cumulative,accuracy)=prob</math>, then <math>GAMMAINV (probability,alpha,beta,accuracy,somenumberofiterations)= x</math>. |
*GAMMAINV use the iterating method to find the value of <math>x</math>. | *GAMMAINV use the iterating method to find the value of <math>x</math>. | ||
*Suppose the iteration has not converged after 100 searches, then the function gives the error result. | *Suppose the iteration has not converged after 100 searches, then the function gives the error result. | ||
| Line 13: | Line 17: | ||
1.Any one of the arguments are non-numeric | 1.Any one of the arguments are non-numeric | ||
2.<math>alpha \le 0 </math> or <math>beta \le 0 </math> | 2.<math>alpha \le 0 </math> or <math>beta \le 0 </math> | ||
| − | 3.<math> | + | 3.<math>probability < 0</math> or <math> probability > 1 </math> |
==Examples== | ==Examples== | ||
| Line 21: | Line 25: | ||
#=GAMMAINV(1,9,3) = 82.51739521528073 | #=GAMMAINV(1,9,3) = 82.51739521528073 | ||
#=GAMMAINV(1.1,9,3) = NAN, because <math> prob>1 </math> | #=GAMMAINV(1.1,9,3) = NAN, because <math> prob>1 </math> | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|SAMTXAAKeug|280|center|GAMMA Distribution}} | ||
==See Also== | ==See Also== | ||
| Line 28: | Line 36: | ||
==References== | ==References== | ||
[http://en.wikipedia.org/wiki/Gamma_distribution Gamma Distribution] | [http://en.wikipedia.org/wiki/Gamma_distribution Gamma Distribution] | ||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 16:12, 7 August 2018
GAMMAINV (probability,alpha,beta,accuracy,somenumberofiterations)
- is the probability value associated with gamma distribution
- & are the values of the shape and rate parameters.
- gives accurate value of the solution.
- is any positive integer.
- GAMMAINV(),returns the inverse of the gamma cumulative distribution.
Description
- This function gives the inverse value of Cumulative Gamma Probability Distribution.
- This distribution is the Continuous Probability Distribution on the positive real line and it is of the reciprocal of a variable distributed according to the gamma distribution with two parameters & .
- It is used in Bayesian statistics.
- In , is the probability value associated with Gamma Distribution, is called shape parameter and is the rate parameter of the distribution.
- If , then .
- GAMMAINV use the iterating method to find the value of .
- Suppose the iteration has not converged after 100 searches, then the function gives the error result.
- This function will give the error result when
1.Any one of the arguments are non-numeric 2. or 3. or
Examples
- =GAMMAINV(0.65189,2,5) = 11.1335534510
- =GAMMAINV(0.006867292,5,7) = 8.155481331
- =GAMMAINV(0.1543869,9,3) = 18.0467153645
- =GAMMAINV(1,9,3) = 82.51739521528073
- =GAMMAINV(1.1,9,3) = NAN, because
Related Videos
See Also
References
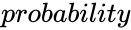 is the probability value associated with gamma distribution
is the probability value associated with gamma distribution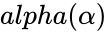 &
& 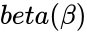 are the values of the shape and rate parameters.
are the values of the shape and rate parameters.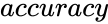 gives accurate value of the solution.
gives accurate value of the solution.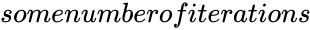 is any positive integer.
is any positive integer.
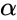 &
& 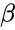 .
.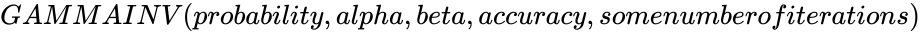 ,
, 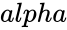 is called shape parameter and
is called shape parameter and  is the rate parameter of the distribution.
is the rate parameter of the distribution.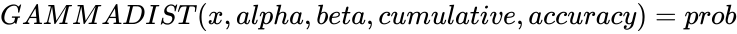 , then
, then 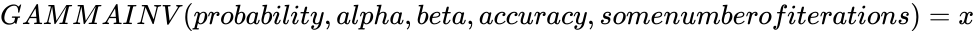 .
. .
.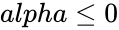 or
or 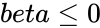 3.
3.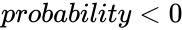 or
or