Difference between revisions of "Manuals/calci/PERMUT"
Jump to navigation
Jump to search
| (14 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''PERMUT( | + | <div style="font-size:30px">'''PERMUT(Number,NumberChosen)'''</div><br/> |
| − | *<math> | + | *<math>Number</math> and <math> NumberChosen </math> are integers. |
| − | + | **PERMUT(), returns the number of permutations for a given number of objects. | |
==Description== | ==Description== | ||
*This function gives the number of Permutations for a given number of objects. | *This function gives the number of Permutations for a given number of objects. | ||
| − | *A permutation, also called an "arrangement number" or "order, | + | *A permutation, also called an "arrangement number" or "order", is a rearrangement of the elements of an ordered list. |
*A selection of objects in which the order of the objects matters. | *A selection of objects in which the order of the objects matters. | ||
| − | *A Permutation is an | + | *A Permutation is an Ordered Combination. |
| − | *In <math>PERMUT( | + | *In <math>PERMUT(Number,NumberChosen)</math>, <math>Number</math> is an integer which is indicating the number of objects and <math>NumberChosen</math> is an integer which is indicating the number of objects in each permutation. |
| − | *For | + | *For <math>Number</math> and <math>NumberChosen</math>, when we give in decimals, it will change into integers. |
| − | *The formula for the number of permutation is:<math>_n P_k= \frac {n!}{(n-k)!}</math> | + | *The formula for the number of permutation is: <math>_n P_k= \frac {n!}{(n-k)!}</math> |
| − | *The Permutation is denoted by <math> _nP_k, P_{n,k}, or P(n,k) </math>.This function will give the result as error when | + | *The Permutation is denoted by <math> _nP_k</math>, <math>P_{n,k}</math>, or <math>P(n,k) </math>.This function will give the result as error when |
| − | 1. | + | 1.<math>Number</math> and <math>NumberChosen</math> are non-numeric. |
| − | 2.Suppose <math> | + | 2.Suppose <math> Number \le 0</math> or <math>NumberChosen < 0</math> or <math>Number < NumberChosen </math>. |
==Examples== | ==Examples== | ||
| − | #PERMUT(14,2)=182 | + | #PERMUT(14,2) = 182 |
| − | #PERMUT(50,5)=254251200 | + | #PERMUT(50,5) = 254251200 |
| − | #PERMUT(10.2,3)=720 | + | #PERMUT(10.2,3) = 720 |
| − | #PERMUT(4,0)=1 | + | #PERMUT(4,0) = 1 |
| − | #PERMUT(6,1)=6 | + | #PERMUT(6,1) = 6 |
| + | #34!P!3 = 35904 | ||
| + | #PERMUT(COMBIN(34, 3n), 3) OR a=34n!C!3!P!3 = 214169191104 | ||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|4AdJeFfHuxY|280|center|PERMUT}} | ||
==See Also== | ==See Also== | ||
| Line 30: | Line 35: | ||
==References== | ==References== | ||
| + | [http://en.wikipedia.org/wiki/Permutation Permutation ] | ||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 03:22, 24 February 2022
PERMUT(Number,NumberChosen)
- and are integers.
- PERMUT(), returns the number of permutations for a given number of objects.
Description
- This function gives the number of Permutations for a given number of objects.
- A permutation, also called an "arrangement number" or "order", is a rearrangement of the elements of an ordered list.
- A selection of objects in which the order of the objects matters.
- A Permutation is an Ordered Combination.
- In , is an integer which is indicating the number of objects and is an integer which is indicating the number of objects in each permutation.
- For and , when we give in decimals, it will change into integers.
- The formula for the number of permutation is:
- The Permutation is denoted by , , or .This function will give the result as error when
1. and are non-numeric. 2.Suppose or or .
Examples
- PERMUT(14,2) = 182
- PERMUT(50,5) = 254251200
- PERMUT(10.2,3) = 720
- PERMUT(4,0) = 1
- PERMUT(6,1) = 6
- 34!P!3 = 35904
- PERMUT(COMBIN(34, 3n), 3) OR a=34n!C!3!P!3 = 214169191104
Related Videos
See Also
References
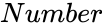 and
and 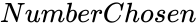 are integers.
are integers.
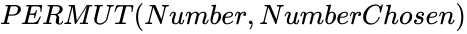 ,
, 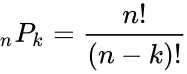
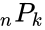 ,
, 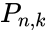 , or
, or 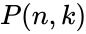 .This function will give the result as error when
.This function will give the result as error when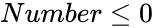 or
or 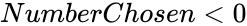 or
or 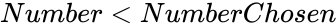 .
.