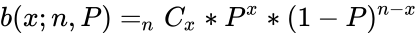Difference between revisions of "Manuals/calci/BINOMIALPROBABILTY"
Jump to navigation
Jump to search
(Created page with "==Feature==") |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | == | + | <div style="font-size:30px">'''BINOMIALPROBABILTY (NumberOftrials,NumberOfSuccess,ProbabiltyOfSuccess)'''</div><br/> |
| + | *<math>NumberOftrials</math> is any number of trials. | ||
| + | |||
| + | |||
| + | ==Description== | ||
| + | *This function shows the value of Binomial Probability. | ||
| + | *In <math>BINOMIALPROBABILTY (NumberOftrials,NumberOfSuccess,ProbabiltyOfSuccess)</math>,<math>NumberOf trials</math> is the number of times of the trials. | ||
| + | *<math>NumberofSuccess</math> is the results of the success. | ||
| + | *<math>ProbabilityOfSuccess</math> is the value of the Probability. | ||
| + | *The binomial probability refers to the probability that a binomial experiment results in exactly x successes. | ||
| + | *Suppose a binomial experiment consists of n trials and results in x successes. | ||
| + | *If the probability of success on an individual trial is P, then the binomial probability is: | ||
| + | <math>b(x; n, P) = _nC_x* P^x *(1 - P)^{n - x}</math> | ||
| + | |||
| + | ==Examples== | ||
| + | #BINOMIALPROBABILTY(5,2,1/6) = 0.1607510288065844 | ||
| + | #BINOMIALPROBABILTY(10,4,1/3)= 0.2276075801453032 | ||
| + | #BINOMIALPROBABILTY(20,19,1/9) = 1.3160421343951921e-17 | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/BINOMIAL | BINOMIAL ]] | ||
| + | *[[Manuals/calci/BINOMIALCOEFFICIENT | BINOMIALCOEFFICIENT]] | ||
| + | *[[Manuals/calci/BINOMIALDISTRIBUTED | BINOMIALDISTRIBUTED ]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://stattrek.com/probability-distributions/binomial.aspx] | ||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 16:28, 27 December 2018
BINOMIALPROBABILTY (NumberOftrials,NumberOfSuccess,ProbabiltyOfSuccess)
- is any number of trials.
Description
- This function shows the value of Binomial Probability.
- In , is the number of times of the trials.
- is the results of the success.
- is the value of the Probability.
- The binomial probability refers to the probability that a binomial experiment results in exactly x successes.
- Suppose a binomial experiment consists of n trials and results in x successes.
- If the probability of success on an individual trial is P, then the binomial probability is:
Examples
- BINOMIALPROBABILTY(5,2,1/6) = 0.1607510288065844
- BINOMIALPROBABILTY(10,4,1/3)= 0.2276075801453032
- BINOMIALPROBABILTY(20,19,1/9) = 1.3160421343951921e-17
See Also
References
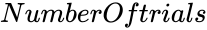 is any number of trials.
is any number of trials.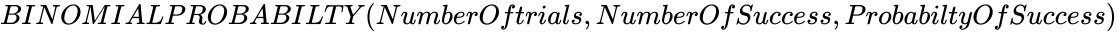 ,
,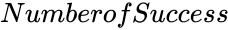 is the results of the success.
is the results of the success.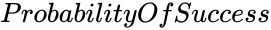 is the value of the Probability.
is the value of the Probability.