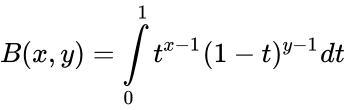Difference between revisions of "Manuals/calci/BETAFUNCTION"
Jump to navigation
Jump to search
| (3 intermediate revisions by 2 users not shown) | |||
| Line 6: | Line 6: | ||
*Beta function is also called the Euler integral of the first kind. | *Beta function is also called the Euler integral of the first kind. | ||
*To evaluate the Beta function we usually use the Gamma function. | *To evaluate the Beta function we usually use the Gamma function. | ||
| − | <math>B(x,y)=\frac{Gamma(x)Gamma(y)}{Gamma(x+y)}</math>. | + | <math>B(x,y)=\frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}</math>. |
*For x,y positive we define the Beta function by: | *For x,y positive we define the Beta function by: | ||
<math>B(x,y)= \int\limits_{0}^{1} t^{x-1}(1-t)^{y-1} dt</math> | <math>B(x,y)= \int\limits_{0}^{1} t^{x-1}(1-t)^{y-1} dt</math> | ||
| + | |||
| + | ==Examples== | ||
| + | #BETAFUNCTION(10,23) = 1.550093439705759e-9 | ||
| + | #BETAFUNCTION(9.1,7.4) = 0.00001484129272494359 | ||
| + | #BETAFUNCTION(876,432) = NaN | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=v1uUgTcInQk|280|center|Beta Function}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/BETADISTX | BETADISTX]] | ||
| + | *[[Manuals/calci/BETAINV | BETAINV]] | ||
| + | |||
| + | ==References== | ||
| + | [http://math.feld.cvut.cz/mt/txtd/5/txe3da5h.htm Beta Function] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 16:04, 4 December 2018
BETAFUNCTION (a,b)
- and are any positive real numbers.
Description
- This function returns the value of the Beta function.
- Beta function is also called the Euler integral of the first kind.
- To evaluate the Beta function we usually use the Gamma function.
.
- For x,y positive we define the Beta function by:
Examples
- BETAFUNCTION(10,23) = 1.550093439705759e-9
- BETAFUNCTION(9.1,7.4) = 0.00001484129272494359
- BETAFUNCTION(876,432) = NaN
Related Videos
See Also
References
 and
and  are any positive real numbers.
are any positive real numbers.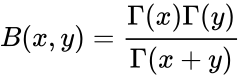 .
.