Difference between revisions of "Manuals/calci/BINOMIALDISTRIBUTED"
Jump to navigation
Jump to search
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''BINOMIALDISTRIBUTED (Numbers,Probability)'''</div><br/> | + | <div style="font-size:30px">'''BINOMIALDISTRIBUTED (Numbers,Probability,Trials)'''</div><br/> |
*<math>Numbers</math> is the number of variables. | *<math>Numbers</math> is the number of variables. | ||
*<math>Probability</math> is the value from 0 to 1. | *<math>Probability</math> is the value from 0 to 1. | ||
| + | *<math>Trials</math> is the any positive real number. | ||
==Description== | ==Description== | ||
*This function gives the value of the Binomial distribution. | *This function gives the value of the Binomial distribution. | ||
| − | *In <math>BINOMIALDISTRIBUTED (Numbers,Probability)</math>, <math>Numbers</math> is the number of the variables and <math>Probability</math> is the probability value which varies from 0 to 1. | + | *In <math>BINOMIALDISTRIBUTED (Numbers,Probability,Trials)</math>, <math>Numbers</math> is the number of the variables and <math>Probability</math> is the probability value which varies from 0 to 1.<math> Trial </math> is any positive real number. |
*This gives the discrete probability distribution. | *This gives the discrete probability distribution. | ||
*The probability of getting exactly k successes in n trials is given by the Probability Mass Function: | *The probability of getting exactly k successes in n trials is given by the Probability Mass Function: | ||
| Line 13: | Line 14: | ||
==Examples== | ==Examples== | ||
| − | #BINOMIALDISTRIBUTED(10,0.4) = 0 | + | # BINOMIALDISTRIBUTED(10,0.4) = 36 42 45 41 41 38 37 36 32 41 |
| + | # BINOMIALDISTRIBUTED(5,0.3,76) = 23 29 20 19 23 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=WWv0RUxDfbs|280|center|Binomial Distribution}} | ||
==See Also== | ==See Also== | ||
Latest revision as of 16:59, 5 December 2018
BINOMIALDISTRIBUTED (Numbers,Probability,Trials)
- is the number of variables.
- is the value from 0 to 1.
- is the any positive real number.
Description
- This function gives the value of the Binomial distribution.
- In , is the number of the variables and is the probability value which varies from 0 to 1. is any positive real number.
- This gives the discrete probability distribution.
- The probability of getting exactly k successes in n trials is given by the Probability Mass Function:
for k=0,1,2,3...n where is the COMBIN(n,k) i.e.
- The Cumulative Binomial Distribution is:.
Examples
- BINOMIALDISTRIBUTED(10,0.4) = 36 42 45 41 41 38 37 36 32 41
- BINOMIALDISTRIBUTED(5,0.3,76) = 23 29 20 19 23
Related Videos
See Also
References
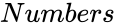 is the number of variables.
is the number of variables.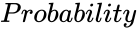 is the value from 0 to 1.
is the value from 0 to 1.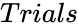 is the any positive real number.
is the any positive real number.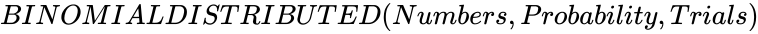 ,
,  is any positive real number.
is any positive real number.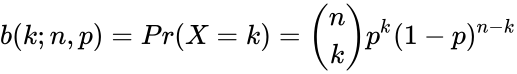 for k=0,1,2,3...n where
for k=0,1,2,3...n where 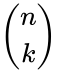 is the COMBIN(n,k) i.e.
is the COMBIN(n,k) i.e.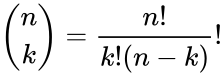
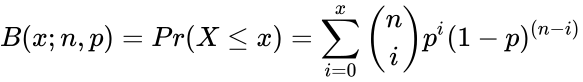 .
.