Difference between revisions of "Manuals/calci/DOTPRODUCT"
Jump to navigation
Jump to search
| (2 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
*Dot product is also called Scalar Product. | *Dot product is also called Scalar Product. | ||
*This product is an example of an Inner product. | *This product is an example of an Inner product. | ||
| + | *Dot product is the algebraic operation which calculates with the two equal length values and gives the single value as result. | ||
| + | *Here a and b are two set of values with any real numbers. | ||
| + | *Also a and b are having same length of values. | ||
*Dot product of two vectors is defined as: <math>a=[a_1,a_2,a_3..a_n]</math> and <math>b=[b_1,b_2,b_3..b_n]</math> then <math>a.b= \sum_{i=1}^n a_{i}b_{i}= a_1b_1+a_2b_2+...a_nb_n</math> where <math>\Sigma</math> denotes summation notation and <math>n</math> is the dimension of the vector space. | *Dot product of two vectors is defined as: <math>a=[a_1,a_2,a_3..a_n]</math> and <math>b=[b_1,b_2,b_3..b_n]</math> then <math>a.b= \sum_{i=1}^n a_{i}b_{i}= a_1b_1+a_2b_2+...a_nb_n</math> where <math>\Sigma</math> denotes summation notation and <math>n</math> is the dimension of the vector space. | ||
| Line 13: | Line 16: | ||
#DOTPRODUCT([-7,-3,5],[101,231,-432]) = -3560 | #DOTPRODUCT([-7,-3,5],[101,231,-432]) = -3560 | ||
#DOTPRODUCT([2/3,8/6,10/3],[2,4,6]) = 26.666666666666664 | #DOTPRODUCT([2/3,8/6,10/3],[2,4,6]) = 26.666666666666664 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=KDHuWxy53uM|280|center|Dot Product}} | ||
==See Also== | ==See Also== | ||
| Line 20: | Line 27: | ||
==References== | ==References== | ||
| − | [http://tutorial.math.lamar.edu/Classes/CalcII/DotProduct.aspx | + | *[http://tutorial.math.lamar.edu/Classes/CalcII/DotProduct.aspx Dot Product] |
Latest revision as of 13:54, 12 December 2018
DOTPRODUCT(a,b)
- and are any two set values.
Description
- This function shows the Dot product of the given numbers.
- Dot product is also called Scalar Product.
- This product is an example of an Inner product.
- Dot product is the algebraic operation which calculates with the two equal length values and gives the single value as result.
- Here a and b are two set of values with any real numbers.
- Also a and b are having same length of values.
- Dot product of two vectors is defined as: and then where denotes summation notation and is the dimension of the vector space.
Examples
- DOTPRODUCT([3,6,9],[10,12,7]) = 165
- DOTPRODUCT([2.5,5.9,6.25],[9,12,13.04]) = 174.8
- DOTPRODUCT([-7,-3,5],[101,231,-432]) = -3560
- DOTPRODUCT([2/3,8/6,10/3],[2,4,6]) = 26.666666666666664
Related Videos
See Also
References
 and
and 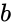 are any two set values.
are any two set values.![{\displaystyle a=[a_{1},a_{2},a_{3}..a_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/png/3c2da4a62501b7e49c80145daa77b1cbb9237250) and
and ![{\displaystyle b=[b_{1},b_{2},b_{3}..b_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/png/34c2103a1c2d3d2665b1dafa8879890e4affb0dd) then
then 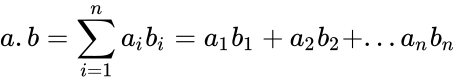 where
where 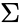 denotes summation notation and
denotes summation notation and  is the dimension of the vector space.
is the dimension of the vector space.