Difference between revisions of "Manuals/calci/SCALARPRODUCT"
Jump to navigation
Jump to search
| (2 intermediate revisions by the same user not shown) | |||
| Line 18: | Line 18: | ||
#SCALARPRODUCT([3.2,4.5,10.3],[4,8,4.3]) = 93.09 | #SCALARPRODUCT([3.2,4.5,10.3],[4,8,4.3]) = 93.09 | ||
#SCALARPRODUCT([-6,-15,21],[32.3,19.3,20.3]) = -56.99999999999994 | #SCALARPRODUCT([-6,-15,21],[32.3,19.3,20.3]) = -56.99999999999994 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=KDHuWxy53uM&t=21s|280|center|Dot Product}} | ||
==See Also== | ==See Also== | ||
| Line 25: | Line 29: | ||
==References== | ==References== | ||
| − | *[http://tutorial.math.lamar.edu/Classes/CalcII/DotProduct.aspx | + | *[http://tutorial.math.lamar.edu/Classes/CalcII/DotProduct.aspx Dot Product] |
*[[Z_API_Functions | List of Main Z Functions]] | *[[Z_API_Functions | List of Main Z Functions]] | ||
*[[ Z3 | Z3 home ]] | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 14:24, 30 January 2019
SCALARPRODUCT(a,b)
DOTPRODUCT(a,b)
- and are any two set values.
Description
- This function shows the Scalar product value.
- In or , and are two set of values with same length.
- Dot product is also called Scalar Product.
- This product is an example of an Inner product.
- Dot product is the algebraic operation which calculates with the two equal length values and gives the single value as result.
- Here a and b are two set of values with any real numbers.
- Also a and b are having same length of values.
- The dot product of two vectors and is defined as:
where denotes summation notation and is the dimension of the vector space.
Examples
- SCALARPRODUCT([2,3,4],[9,8,7]) = 70
- SCALARPRODUCT([3.2,4.5,10.3],[4,8,4.3]) = 93.09
- SCALARPRODUCT([-6,-15,21],[32.3,19.3,20.3]) = -56.99999999999994
 and
and 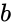 are any two set values.
are any two set values. or
or 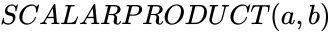 ,
,![{\displaystyle a=[a_{1},a_{2},...,a_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/png/803e8377a0347f4bdd765afc67d41ba8c37d2b8c) and
and ![{\displaystyle b=[b_{1},b_{2},...,b_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/png/6b883f746782dc2b06344d9298c02dc25bb0cc07) is defined as:
is defined as: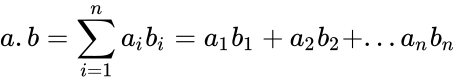 where
where 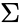 denotes summation notation and
denotes summation notation and  is the dimension of the vector space.
is the dimension of the vector space.