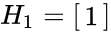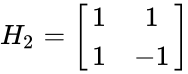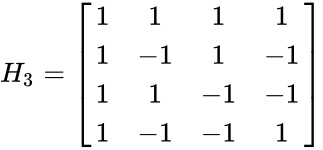Difference between revisions of "Manuals/calci/hadamard"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''MATRIX("HADAMARD",order)'''</div><br/> *<math>order</math> is the order of the hadamard matrix. ==Description== *This function gives the matrix...") |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">''' | + | <div style="font-size:30px">'''HADAMARD(Number)'''</div><br/> |
| − | *<math> | + | *<math>Number</math> is the order of the hadamard matrix. |
==Description== | ==Description== | ||
| Line 26: | Line 26: | ||
1 & -1 & -1 & 1\\ | 1 & -1 & -1 & 1\\ | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
| + | |||
| + | ==Examples== | ||
| + | 1. HADAMARD(1) = 1 | ||
| + | |||
| + | 2. HADAMARD(3) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || 1 || 1 || 1 | ||
| + | |- | ||
| + | | 1 || -1 || 1 || -1 | ||
| + | |- | ||
| + | | 1 || 1 || -1 || -1 | ||
| + | |- | ||
| + | |1 || -1 ||-1 || 1 | ||
| + | |} | ||
| + | 3. HADAMARD(4) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 1 || 1 || 1 || 1 || 1|| 1 || 1 || 1 | ||
| + | |- | ||
| + | | 1 ||-1 ||1 || -1 ||1 ||-1 || 1 ||-1 | ||
| + | |- | ||
| + | |1 || 1 ||-1|| -1|| 1 || 1|| -1||-1 | ||
| + | |- | ||
| + | |1||-1 ||-1|| 1|| 1||-1 || -1 ||1 | ||
| + | |- | ||
| + | |1 || 1 || 1|| 1 || -1 || -1||-1||-1 | ||
| + | |- | ||
| + | |1 ||-1 || 1 || -1 || -1 || 1|| -1||1 | ||
| + | |- | ||
| + | |1 || 1 || -1 || -1 || -1|| -1||1 ||1 | ||
| + | |- | ||
| + | |1 || -1 || -1|| 1 || -1||1|| 1||-1 | ||
| + | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=BM6TUF5dp9c|280|center|Hadamard Matrix}} | ||
| + | |||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/HADAMARD| HADAMARD]] | ||
| + | *[[Manuals/calci/CONFERENCE| CONFERENCE]] | ||
| + | *[[Manuals/calci/CIRCULANT| CIRCULANT]] | ||
| + | *[[Manuals/calci/HANKEL| HANKEL]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://en.wikipedia.org/wiki/Hadamard_matrix Hadamard matrix] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 12:47, 9 April 2019
HADAMARD(Number)
- is the order of the hadamard matrix.
Description
- This function gives the matrix satisfying the property of Hadamard.
- A Hadamard matrix is the square matrix with the entries of 1 and -1.
- Also the rows of that matrix are orthogonal.
- So H be a Hadamard matrix of order 2n.
- The transpose of H is closely related to its inverse.
- The equivalent definition for hadamard matrix is:
where is the n × n identity matrix and is the transpose of H.
- So the possible order of the matrix is 1,2 or positive multiple of 4.
- The few examples of hadamard matrices are:
Examples
1. HADAMARD(1) = 1
2. HADAMARD(3)
| 1 | 1 | 1 | 1 |
| 1 | -1 | 1 | -1 |
| 1 | 1 | -1 | -1 |
| 1 | -1 | -1 | 1 |
3. HADAMARD(4)
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 |
| 1 | 1 | -1 | -1 | 1 | 1 | -1 | -1 |
| 1 | -1 | -1 | 1 | 1 | -1 | -1 | 1 |
| 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 |
| 1 | -1 | 1 | -1 | -1 | 1 | -1 | 1 |
| 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 |
| 1 | -1 | -1 | 1 | -1 | 1 | 1 | -1 |
Related Videos
See Also
References
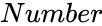 is the order of the hadamard matrix.
is the order of the hadamard matrix.
 is the n × n identity matrix and
is the n × n identity matrix and 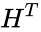 is the transpose of H.
is the transpose of H.