Difference between revisions of "Manuals/calci/GFUNCTION"
Jump to navigation
Jump to search
| (6 intermediate revisions by the same user not shown) | |||
| Line 9: | Line 9: | ||
*According to elementary factors, it is a special case of the double gamma function. | *According to elementary factors, it is a special case of the double gamma function. | ||
*Formally, the Barnes G-function is defined in the following Weierstrass product form: | *Formally, the Barnes G-function is defined in the following Weierstrass product form: | ||
| − | <math>G(1+z)={(2\pi)}^\frac{z}{2}exp(-\frac{z+z^2(1+\gamma)}{2}) | + | <math>G(1+z)={(2\pi)}^\frac{z}{2}exp(-\frac{z+z^2(1+\gamma)}{2})\prod_{k=1}^\infty [{(1+\frac{z}{k})}^k exp(\frac {z^2}{2k}-z)]</math> |
| − | |||
| − | |||
| − | + | ||
| + | ==Examples== | ||
| + | # GFUNCTION(10) = 5056584744960000 | ||
| + | # GFUNCTION(4) = 2 | ||
| + | # GFUNCTION(7) = 34560 | ||
| + | # GFUNCTION(5.2) = 12 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=XZIVrkkYBRI&t=101s|280|center|Gamma Function}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/BETAFUNCTION | BETAFUNCTION]] | ||
| + | *[[Manuals/calci/KFUNCTION | KFUNCTION ]] | ||
| + | |||
| + | ==References== | ||
| + | *[https://en.wikipedia.org/wiki/Barnes_G-function G Function] | ||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 15:02, 22 February 2019
GFUNCTION (Number)
- is any positive real number.
Description
- This function shows the value of the Barnes G-function value.
- In , is any real number.
- is a function that is an extension of super factorials to the complex numbers.
- It is related to the Gamma function, the K-function and the Glaisher–Kinkelin constant, and was named after mathematician Ernest William Barnes.
- According to elementary factors, it is a special case of the double gamma function.
- Formally, the Barnes G-function is defined in the following Weierstrass product form:
Examples
- GFUNCTION(10) = 5056584744960000
- GFUNCTION(4) = 2
- GFUNCTION(7) = 34560
- GFUNCTION(5.2) = 12
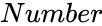 is any positive real number.
is any positive real number.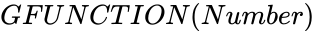 ,
,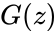 is a function that is an extension of super factorials to the complex numbers.
is a function that is an extension of super factorials to the complex numbers.![{\displaystyle G(1+z)={(2\pi )}^{\frac {z}{2}}exp(-{\frac {z+z^{2}(1+\gamma )}{2}})\prod _{k=1}^{\infty }[{(1+{\frac {z}{k}})}^{k}exp({\frac {z^{2}}{2k}}-z)]}](https://wikimedia.org/api/rest_v1/media/math/render/png/d5b489a14ad6c8b6ef4a38b7cdee963e55211730)