Difference between revisions of "Manuals/calci/LISSAJOUS"
| (One intermediate revision by the same user not shown) | |||
| Line 15: | Line 15: | ||
==Examples== | ==Examples== | ||
| + | # LISSAJOUS("circle",4..6) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 4.999998731727338 || 1 | ||
| + | |- | ||
| + | |4.98033339924072 || 1.3993336665873126 | ||
| + | |- | ||
| + | |4.9208978911521815 || 1.7946773231802449 | ||
| + | |- | ||
| + | |4.822286067411776 || 2.1820808266453584 | ||
| + | |- | ||
| + | |4.685483224765582 || 2.5576733692346023 | ||
| + | |- | ||
| + | |4.511856251996312 || 2.917702154416812 | ||
| + | |- | ||
| + | |4.303139972422432 || 3.2585698935801415 | ||
| + | |- | ||
| + | |4.061419810117014 || 3.576870748950764 | ||
| + | |- | ||
| + | |3.789110953039751 || 3.8694243635980907 | ||
| + | |- | ||
| + | |3.48893422127722 || 4.133307638509933 | ||
| + | |- | ||
| + | |3.163888881507954 || 4.365883939231585 | ||
| + | |- | ||
| + | |2.817222679321226 || 4.564829440245742 | ||
| + | |- | ||
| + | |2.4523993888166733 || 4.728156343868905 | ||
| + | |- | ||
| + | |2.073064203718472 || 4.854232741668772 | ||
| + | |} | ||
| + | and so on. | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=K_MVFYyVkXQ|280|center|Lissajous}} | ||
==See Also== | ==See Also== | ||
| Line 20: | Line 56: | ||
*[[Manuals/calci/FRACTAL | FRACTAL ]] | *[[Manuals/calci/FRACTAL | FRACTAL ]] | ||
*[[Manuals/calci/LISSAJOUSCURVE| LISSAJOUSCURVE ]] | *[[Manuals/calci/LISSAJOUSCURVE| LISSAJOUSCURVE ]] | ||
| − | |||
==References== | ==References== | ||
Latest revision as of 14:58, 28 February 2019
LISSAJOUS (TypeOrSettings,AsTable)
- is any type like Ellipse or circle and so on.
Description
- This function shows the values of the Lissajous curve.
- Lissajous Curve is a parametric plot of the harmonic system.
- It is also called Bowditch Curves.
- Lissajous used sounds of different frequencies to vibrate a mirror.
- A beam of light reflected from the mirror, was allowed to trace patterns which depended on the frequencies of the sounds – in a setup similar to projectors used in today's laser light shows.Lissajous figure is the intersection of two sinusoidal curves, the axes of which are at right angles to each other.
- Mathematically, this translates to a Complex harmonic function: In the Lissajous equation,a=1,b=1,A=1,B=1 and = radians, the figure is a circle.
- So these values substitute in the equation and it will shows the result.With the above values when =0,then the value will show for line.
- In the same way the ratio =1 and =0,then the values will be shown for ellipse.
- Suppose = 2, = , then the values will show for parabola.
- The Lissajous curve gets more complicated for other ratios, which are closed only if a/b is rational.
Examples
- LISSAJOUS("circle",4..6)
| 4.999998731727338 | 1 |
| 4.98033339924072 | 1.3993336665873126 |
| 4.9208978911521815 | 1.7946773231802449 |
| 4.822286067411776 | 2.1820808266453584 |
| 4.685483224765582 | 2.5576733692346023 |
| 4.511856251996312 | 2.917702154416812 |
| 4.303139972422432 | 3.2585698935801415 |
| 4.061419810117014 | 3.576870748950764 |
| 3.789110953039751 | 3.8694243635980907 |
| 3.48893422127722 | 4.133307638509933 |
| 3.163888881507954 | 4.365883939231585 |
| 2.817222679321226 | 4.564829440245742 |
| 2.4523993888166733 | 4.728156343868905 |
| 2.073064203718472 | 4.854232741668772 |
and so on.
Related Videos
See Also
References
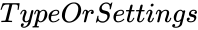 is any type like Ellipse or circle and so on.
is any type like Ellipse or circle and so on.