Difference between revisions of "Manuals/calci/MANDELBROT"
Jump to navigation
Jump to search
| Line 12: | Line 12: | ||
#MANDELBROT() | #MANDELBROT() | ||
[[File:Mandelbrot.png]] | [[File:Mandelbrot.png]] | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=8ma6cV6fw24|280|center|Mandel brot}} | ||
| + | |||
==See Also== | ==See Also== | ||
| Line 17: | Line 22: | ||
*[[Manuals/calci/LISSAJOUSCURVE| LISSAJOUSCURVE ]] | *[[Manuals/calci/LISSAJOUSCURVE| LISSAJOUSCURVE ]] | ||
*[[Manuals/calci/LISSAJOUS| LISSAJOUS ]] | *[[Manuals/calci/LISSAJOUS| LISSAJOUS ]] | ||
| − | |||
==References== | ==References== | ||
Latest revision as of 14:47, 4 March 2019
MANDELBROT (SettingsArray,Width,Height,MandeliterFunction,Shades,CanvasId)
Description
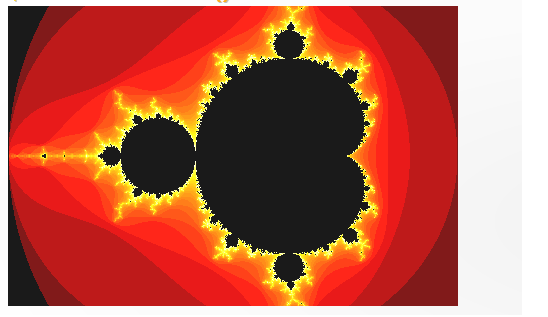
- This function shows the figure of the Mandelbrot.
- Fractals are infinitely complex patterns that are self-similar across different scales.
- This property is called self-similarity.
- Fractals form a never ending pattern, created by repeating a simple process over and over, in an ongoing feedback loop.Mandelbrot Set is the set of points in the complex plane with the sequence where the result does not approach infinity.
- The Julia Set is closely related to Mandelbrot Set.
- The Mandelbrot Set is obtained from the quadratic recurrence equation , (with=0), where points c in the complex plane for which the computed value of does not tend to infinity.
Examples
- MANDELBROT()
Related Videos
See Also
References
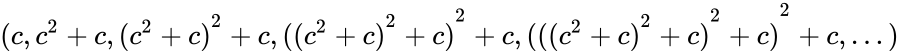 where the result does not approach infinity.
where the result does not approach infinity.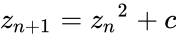 , (with
, (with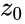 =0), where points c in the complex plane for which the computed value of
=0), where points c in the complex plane for which the computed value of 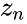 does not tend to infinity.
does not tend to infinity.