Difference between revisions of "Manuals/calci/TORUS"
(Created page with "<div style="font-size:30px">'''TORUS (Radius,TubeRadius,w1) '''</div><br/> *<math>Radius</math> and <math>TubeRadius</math> are radius value of the circle. ==Description== *T...") |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''TORUS (Radius,TubeRadius,w1) '''</div><br/> | + | <div style="font-size:30px">'''TORUS (Radius,TubeRadius,w1)'''</div><br/> |
| + | where | ||
*<math>Radius</math> and <math>TubeRadius</math> are radius value of the circle. | *<math>Radius</math> and <math>TubeRadius</math> are radius value of the circle. | ||
| + | **TORUS() shows the Torus for the given value. | ||
==Description== | ==Description== | ||
| − | + | TORUS (Radius,TubeRadius,w1) | |
| − | + | *<math>Radius</math> is the radius value of the bigger circle. | |
*<math>TubeRadius</math> is the radius value of the smaller circle. | *<math>TubeRadius</math> is the radius value of the smaller circle. | ||
*A torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis co planar with the circle. *If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution. | *A torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis co planar with the circle. *If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution. | ||
*For example of TORUS are rings, doughnuts, and bagels. | *For example of TORUS are rings, doughnuts, and bagels. | ||
*A torus can be defined parametrically by: | *A torus can be defined parametrically by: | ||
| − | <math>x(\theta,\phi)=(R+rCos\theta)Cos\phi</math> | + | <math>x(\theta,\phi)=(R+rCos\theta)Cos\phi</math> |
| + | <math>y(\theta,\phi)=(R+rCos\theta)Sin\phi</math> | ||
| + | <math>z(\theta,\phi)=r Sin\theta</math> | ||
where | where | ||
| − | + | <math>\theta</math>,<math>\phi</math> are angles which make a full circle, so that their values start and end at the same point. | |
| − | R is the distance from the center of the tube to the center of the torus | + | *<math>R</math> is the distance from the center of the tube to the center of the torus. |
| − | r is the radius of the tube. | + | *<math>r</math> is the radius of the tube. |
| − | R is known as the | + | *<math>R</math> is known as the "major radius" and <math>r</math> is known as the "minor radius". |
| + | *The ratio R divided by r is known as the aspect ratio. | ||
| + | *The typical doughnut confectionery has an aspect ratio of about 3 to 2. | ||
| + | |||
| + | ==Examples== | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=q6zvITS0hi0|280|center|Torus}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/FRACTAL | FRACTAL ]] | ||
| + | *[[Manuals/calci/LISSAJOUS | LISSAJOUS ]] | ||
| + | *[[Manuals/calci/SURFACEGRAPH| SURFACEGRAPH ]] | ||
| + | |||
| + | ==References== | ||
| + | *[https://en.wikipedia.org/wiki/Torus Torus] | ||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 14:28, 4 March 2019
TORUS (Radius,TubeRadius,w1)
where
- and are radius value of the circle.
- TORUS() shows the Torus for the given value.
Description
TORUS (Radius,TubeRadius,w1)
- is the radius value of the bigger circle.
- is the radius value of the smaller circle.
- A torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis co planar with the circle. *If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution.
- For example of TORUS are rings, doughnuts, and bagels.
- A torus can be defined parametrically by:
where , are angles which make a full circle, so that their values start and end at the same point.
- is the distance from the center of the tube to the center of the torus.
- is the radius of the tube.
- is known as the "major radius" and is known as the "minor radius".
- The ratio R divided by r is known as the aspect ratio.
- The typical doughnut confectionery has an aspect ratio of about 3 to 2.
Examples
Related Videos
See Also
References
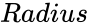 and
and 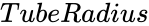 are radius value of the circle.
are radius value of the circle.