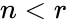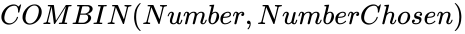Difference between revisions of "Manuals/calci/COMBIN"
Jump to navigation
Jump to search
(Created page with "<div id="16SpaceContent" align="left"><div class="ZEditBox" align="justify"> Syntax </div></div> ---- <div id="4SpaceContent" align="left"><div class="ZEditBox" align=...") |
|||
| (53 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''COMBIN(Number,Numberchosen)'''</div><br/> |
| − | + | *<math>Number</math> is the number of items. | |
| + | *<math>NumberChosen</math> is the number of items in each arrangement. | ||
| + | **COMBIN() returns the number of combinations for a given number of objects. | ||
| − | </ | + | ==Description== |
| − | - | + | *This function gives the combination of the given number of objects. |
| − | < | + | *Let Number be "n" and Number chosen be "r". |
| + | *So the Combinations is an arrangement of <math>r</math> objects without any repetition, selected from <math>n</math> different objects is called a combination of <math>n</math> objects taken <math>r</math> at a time. | ||
| + | *For example consider three colors, like Blue,Yellow,Pink.There are three combinations of two can be drawn from the set:Blue and Yellow,Blue and Pink,or Yellow and Pink. | ||
| + | *If the order is not a matter, it is a Combination. | ||
| + | *If the order is a matter it is a Permutation. | ||
| + | *A combination is denoted by <math>^nC_r</math> or <math>\binom{n}{r}</math> or <math>C(n,r)</math>. | ||
| + | *A formula for the number of possible combinations of <math>r</math> objects from a set of <math>n</math> objects is: | ||
| + | <math>\binom{n}{r}=\frac{n!}{r!(n-r)!}</math> | ||
| + | where <math>n!=1*2*3*...*n </math> & <math>r \le n</math>. | ||
| + | *This function will give Error Result when | ||
| + | #The <math>n</math> & <math>r</math> are non numeric | ||
| + | #The <math>n</math> & <math>r < 0 </math> or <math>n < r</math> | ||
| + | *When we are giving the <math>n</math> & <math>r</math> values in decimals, it will truncated into Integers. | ||
| + | *For e.g. | ||
| + | **COMBIN(5.4,2)=10 is equivalent to COMBIN(5,2) | ||
| + | **COMBIN(5,-2)=#N/A (NUMBERCHOSEN > 0), because <math>r</math> is negative. | ||
| − | + | ==ZOS== | |
| + | *The syntax is to calculate COMBIN in ZOS is <math>COMBIN(Number,NumberChosen)</math> | ||
| + | **<math>Number</math> is the number of items. | ||
| + | **<math>NumberChosen</math> is the number of items in each arrangement. | ||
| + | **For e.g.,COMBIN(20..23,6..7) | ||
| + | **COMBIN(4,2)*COMBIN(10,5) | ||
| + | **COMBIN(12.3,3) gives 220, though COMBIN(12.3d,3n) gives 238.5995. Here, the use of higher number types (like big number, decimal, etc.) different logic is triggered. In base plain numbers and Number objects, the numbers are truncated. | ||
| − | + | {{#ev:youtube|cQXPq6y8bOw|280|center|Combin}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ==Examples== | ||
{| id="TABLE3" class="SpreadSheet blue" | {| id="TABLE3" class="SpreadSheet blue" | ||
|- class="even" | |- class="even" | ||
| − | | | + | | COMBIN(Number,NumberChosen) |
| − | + | ! Number | |
| − | + | ! Numberchosen | |
| − | + | ! RESULT | |
| − | + | |- | |
| − | |||
| − | |- | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- class="odd" | |- class="odd" | ||
| − | | | + | |COMBIN(12,3) |
| − | | | + | |12 |
| − | + | |3 | |
| − | | | + | |220 |
| − | | | ||
| − | |||
|- class="even" | |- class="even" | ||
| − | | | + | |COMBIN(4,4) |
| − | | | + | |4 |
| − | + | |4 | |
| − | | | + | |1 |
| − | | | ||
|- class="odd" | |- class="odd" | ||
| − | | | + | |COMBIN(4,0) |
| − | + | |4 | |
| − | + | |0 | |
| − | + | |1 | |
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| + | a=34!C!3 | ||
| + | 5984 | ||
| + | |||
| + | COMBIN(PERMUT(34, 3n), 3) (For Big Integer) OR a=34n!P!3!C!3 = 7713313203904 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|Bzuj8ItKT5w|280|center|COMBIN}} | ||
| + | |||
| + | ==See Also== | ||
| − | + | *[[Manuals/calci/FACT | FACT]] | |
| − | + | *[[Manuals/calci/PERMUT | PERMUT ]] | |
| − | |||
| − | + | ==References== | |
| + | [http://en.wikipedia.org/wiki/Combination Combination] | ||
| − | |||
| − | |||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| − | + | *[[ Z3 | Z3 home ]] | |
| − | |||
| − | |||
Latest revision as of 04:18, 24 February 2022
COMBIN(Number,Numberchosen)
- is the number of items.
- is the number of items in each arrangement.
- COMBIN() returns the number of combinations for a given number of objects.
Description
- This function gives the combination of the given number of objects.
- Let Number be "n" and Number chosen be "r".
- So the Combinations is an arrangement of objects without any repetition, selected from different objects is called a combination of objects taken at a time.
- For example consider three colors, like Blue,Yellow,Pink.There are three combinations of two can be drawn from the set:Blue and Yellow,Blue and Pink,or Yellow and Pink.
- If the order is not a matter, it is a Combination.
- If the order is a matter it is a Permutation.
- A combination is denoted by or or .
- A formula for the number of possible combinations of objects from a set of objects is:
where & .
- This function will give Error Result when
- The & are non numeric
- The & or
- When we are giving the & values in decimals, it will truncated into Integers.
- For e.g.
- COMBIN(5.4,2)=10 is equivalent to COMBIN(5,2)
- COMBIN(5,-2)=#N/A (NUMBERCHOSEN > 0), because is negative.
ZOS
- The syntax is to calculate COMBIN in ZOS is
- is the number of items.
- is the number of items in each arrangement.
- For e.g.,COMBIN(20..23,6..7)
- COMBIN(4,2)*COMBIN(10,5)
- COMBIN(12.3,3) gives 220, though COMBIN(12.3d,3n) gives 238.5995. Here, the use of higher number types (like big number, decimal, etc.) different logic is triggered. In base plain numbers and Number objects, the numbers are truncated.
Examples
| COMBIN(Number,NumberChosen) | Number | Numberchosen | RESULT |
|---|---|---|---|
| COMBIN(12,3) | 12 | 3 | 220 |
| COMBIN(4,4) | 4 | 4 | 1 |
| COMBIN(4,0) | 4 | 0 | 1 |
a=34!C!3 5984
COMBIN(PERMUT(34, 3n), 3) (For Big Integer) OR a=34n!P!3!C!3 = 7713313203904
Related Videos
See Also
References
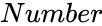 is the number of items.
is the number of items.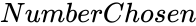 is the number of items in each arrangement.
is the number of items in each arrangement.
 objects without any repetition, selected from
objects without any repetition, selected from  different objects is called a combination of
different objects is called a combination of 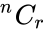 or
or 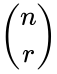 or
or 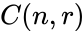 .
.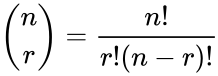
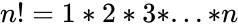 &
&  .
.
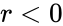 or
or