Difference between revisions of "Manuals/calci/DCOSEC"
Jump to navigation
Jump to search
| (11 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''DCOSEC( | + | <div style="font-size:30px">'''DCOSEC(Number)'''</div><br/> |
| − | * | + | * <math>Number</math> is the angle in degrees. |
| − | * | + | **DCOSEC(),returns the double-precision cosecant of the given angle |
| − | [[Manuals/calci/COSEC| COSEC]] can be used if the angle is in Radians. | + | |
| + | [[Manuals/calci/COSEC| COSEC]] can be used if the angle is in Radians.<br/> | ||
| + | The angle can be a single value or any complex array of values.<br/> | ||
| + | For example DCOSEC(1..100) can give an array of the results, which is the COSECANT value for each of the elements in the array. The array could be of any values either '+' or '-' like 1..5@DCOSEC or (-5)..(-1)@DCOSEC. | ||
| + | |||
==Description== | ==Description== | ||
| − | *This function is used to obtain the Cosecant value of | + | *This function is used to obtain the Cosecant value of any Number in degrees. |
| − | *It is the reciprocal of SIN function i.e, '''COSEC(x) = 1 / SIN(x)''' | + | *It is the reciprocal of SIN function i.e, '''COSEC(x) = 1 / SIN(x)''' |
| − | *In a right angled triangle '''COSEC(x) = Hypotenuse / Opposite side'''. | + | *In a right angled triangle '''COSEC(x) = Hypotenuse / Opposite side'''. |
*To obtain the value in Radians multiply with PI()/180 or use COSEC function COSEC(X) | *To obtain the value in Radians multiply with PI()/180 or use COSEC function COSEC(X) | ||
*DCOSEC returns NaN if 'x' is not real | *DCOSEC returns NaN if 'x' is not real | ||
| − | |||
| − | The following example shows how DCOSEC is applied to an array of numbers containing | + | The following example shows how DCOSEC is applied to an array of numbers containing angles 1..10. |
*Type =1..10@DCOSEC in Calci | *Type =1..10@DCOSEC in Calci | ||
*Type =1..10@DCOSEC or 1..10@DCOSEC in ZOS | *Type =1..10@DCOSEC or 1..10@DCOSEC in ZOS | ||
| Line 18: | Line 21: | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| − | ! | + | ! Angles !! DCOSEC |
|- | |- | ||
| 1 || 57.2986884985501 | | 1 || 57.2986884985501 | ||
| Line 42: | Line 45: | ||
== Examples == | == Examples == | ||
| − | '''DCOSEC( | + | '''DCOSEC(Number)''' |
| − | *''' | + | *'''Number''' is the angle in Degrees. |
* Result shows DCOSEC(abc)= NAN | * Result shows DCOSEC(abc)= NAN | ||
| Line 49: | Line 52: | ||
|- class="even" | |- class="even" | ||
| − | |'''DCOSEC( | + | |'''DCOSEC(Degrees)''' |
|'''Value''' | |'''Value''' | ||
|- class="odd" | |- class="odd" | ||
| − | | DCOSEC( | + | | DCOSEC(0) |
| − | | | + | | infinity |
|- class="even" | |- class="even" | ||
| − | | DCOSEC( | + | | DCOSEC(1) |
| − | | | + | | 57.298688498550185 |
|- class="odd" | |- class="odd" | ||
| − | | DCOSEC( | + | | DCOSEC(90) |
| − | | | + | | 1 |
|} | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|Kz6tCMgat94|280|center|Trig Function Values in Degrees}} | ||
==See Also== | ==See Also== | ||
| − | *[[Manuals/calci/ | + | *[[Manuals/calci/COSEC | COSEC]] |
| − | *[[Manuals/calci/ | + | *[[Manuals/calci/SIN | SIN]] |
| − | *[[Manuals/calci/ | + | *[[Manuals/calci/ASIN| ASIN]] |
| − | |||
| − | |||
==References== | ==References== | ||
*[http://en.wikipedia.org/wiki/Trigonometric_functions List of Trigonometric Functions] | *[http://en.wikipedia.org/wiki/Trigonometric_functions List of Trigonometric Functions] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 15:18, 25 June 2018
DCOSEC(Number)
- is the angle in degrees.
- DCOSEC(),returns the double-precision cosecant of the given angle
COSEC can be used if the angle is in Radians.
The angle can be a single value or any complex array of values.
For example DCOSEC(1..100) can give an array of the results, which is the COSECANT value for each of the elements in the array. The array could be of any values either '+' or '-' like 1..5@DCOSEC or (-5)..(-1)@DCOSEC.
Description
- This function is used to obtain the Cosecant value of any Number in degrees.
- It is the reciprocal of SIN function i.e, COSEC(x) = 1 / SIN(x)
- In a right angled triangle COSEC(x) = Hypotenuse / Opposite side.
- To obtain the value in Radians multiply with PI()/180 or use COSEC function COSEC(X)
- DCOSEC returns NaN if 'x' is not real
The following example shows how DCOSEC is applied to an array of numbers containing angles 1..10.
- Type =1..10@DCOSEC in Calci
- Type =1..10@DCOSEC or 1..10@DCOSEC in ZOS
| Angles | DCOSEC |
|---|---|
| 1 | 57.2986884985501 |
| 2 | 28.65370835 |
| 3 | 19.10732261 |
| 4 | 14.33558703 |
| 5 | 11.47371325 |
| 6 | 9.566772234 |
| 7 | 8.205509048 |
| 8 | 7.185296534 |
| 9 | 6.392453221 |
| 10 | 5.758770483 |
Examples
DCOSEC(Number)
- Number is the angle in Degrees.
- Result shows DCOSEC(abc)= NAN
| DCOSEC(Degrees) | Value |
| DCOSEC(0) | infinity |
| DCOSEC(1) | 57.298688498550185 |
| DCOSEC(90) | 1 |
Related Videos
See Also
References
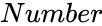 is the angle in degrees.
is the angle in degrees.