Difference between revisions of "Manuals/calci/PERMUT"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''PERMUT(n,nc)'''</div><br/> | <div style="font-size:30px">'''PERMUT(n,nc)'''</div><br/> | ||
*<math>n</math> and <math> nc </math> are integers | *<math>n</math> and <math> nc </math> are integers | ||
| − | |||
==Description== | ==Description== | ||
| Line 8: | Line 7: | ||
*A selection of objects in which the order of the objects matters. | *A selection of objects in which the order of the objects matters. | ||
*A Permutation is an ordered Combination. | *A Permutation is an ordered Combination. | ||
| − | *In <math>PERMUT(n,nc), n</math> is an integer which is indicating the number of objects and nc is an integer which is indicating the number of objects in each permutation. | + | *In <math>PERMUT(n,nc)</math>, <math>n</math> is an integer which is indicating the number of objects and <math>nc</math> is an integer which is indicating the number of objects in each permutation. |
| − | *For n and nc ,when we are giving in to decimals it will change in to integers. | + | *For <math>n</math> and <math>nc</math> ,when we are giving in to decimals it will change in to integers. |
*The formula for the number of permutation is:<math>_n P_k= \frac {n!}{(n-k)!}</math> | *The formula for the number of permutation is:<math>_n P_k= \frac {n!}{(n-k)!}</math> | ||
| − | *The Permutation is denoted by <math> _nP_k, P_{n,k}, or P(n,k) </math>.This function will give the result as error when | + | *The Permutation is denoted by <math> _nP_k</math>, <math>P_{n,k}</math>, or <math>P(n,k) </math>.This function will give the result as error when |
| − | 1.n and nc are | + | 1.<math>n</math> and <math>nc</math> are non-numeric. |
| − | 2.Suppose <math> n \le 0 or nc < 0 or n < nc </math>. | + | 2.Suppose <math> n \le 0</math> or <math>nc < 0</math> or <math>n < nc </math>. |
==Examples== | ==Examples== | ||
Revision as of 04:07, 7 January 2014
PERMUT(n,nc)
- and are integers
Description
- This function gives the number of Permutations for a given number of objects.
- A permutation, also called an "arrangement number" or "order," is a rearrangement of the elements of an ordered list.
- A selection of objects in which the order of the objects matters.
- A Permutation is an ordered Combination.
- In , is an integer which is indicating the number of objects and is an integer which is indicating the number of objects in each permutation.
- For and ,when we are giving in to decimals it will change in to integers.
- The formula for the number of permutation is:
- The Permutation is denoted by , , or .This function will give the result as error when
1. and are non-numeric. 2.Suppose or or .
Examples
- PERMUT(14,2)=182
- PERMUT(50,5)=254251200
- PERMUT(10.2,3)=720
- PERMUT(4,0)=1
- PERMUT(6,1)=6
 and
and 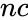 are integers
are integers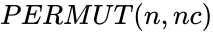 ,
, 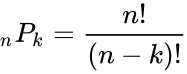
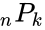 ,
, 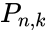 , or
, or 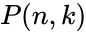 .This function will give the result as error when
.This function will give the result as error when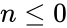 or
or 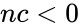 or
or 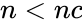 .
.