Difference between revisions of "Manuals/calci/PASCALTRIANGLE"
Jump to navigation
Jump to search
| Line 10: | Line 10: | ||
*The construction is related to the binomial coefficients by Pascal's rule is : | *The construction is related to the binomial coefficients by Pascal's rule is : | ||
<math>(x+y)^n=\sum_{k=0}^n \binom{n}{k}x^{n-k} .y^k </math>. where <math> \dbinom{n}{k}</math> is the binomial coefficient. | <math>(x+y)^n=\sum_{k=0}^n \binom{n}{k}x^{n-k} .y^k </math>. where <math> \dbinom{n}{k}</math> is the binomial coefficient. | ||
| − | *This function will return the result as error when | + | *This function will return the result as error when <math> r \le 0</math>. |
==Examples== | ==Examples== | ||
Revision as of 23:16, 7 January 2014
PASCALTRIANGLE(r)
- is the row number.
Description
- This function gives the Coefficients of the Pascal triangle.
- In , r is the row number of the Pascal triangle.
- Pascal triangle is the arrangement of numbers of the Binomial coefficients in a triangular shape.
- It is started with the number 1 at the top in the 1st row.
- Then from the 2nd row each number in the triangle is the sum of the two directly above it.
- The construction is related to the binomial coefficients by Pascal's rule is :
. where is the binomial coefficient.
- This function will return the result as error when .
Examples
- 1.=PASCALTRIANGLE(1)
1
- 2.=PASCALTRIANGLE(2)
1
1 1
- 3.=PASCALTRIANGLE(3)
1
1 1
1 2 1
- 4.=PASCALTRIANGLE(0) = NULL
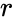 is the row number.
is the row number.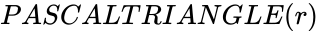 , r is the row number of the Pascal triangle.
, r is the row number of the Pascal triangle.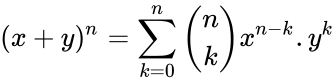 . where
. where 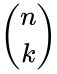 is the binomial coefficient.
is the binomial coefficient.
 .
.