Difference between revisions of "Manuals/calci/IMLN"
Jump to navigation
Jump to search
| Line 10: | Line 10: | ||
*If <math>z = x+iy</math> with <math>x</math> & <math>y</math> are real numbers then natural logarithm of a complex number : | *If <math>z = x+iy</math> with <math>x</math> & <math>y</math> are real numbers then natural logarithm of a complex number : | ||
<math>ln(z)= w = ln(|z|) + iarg(z) = ln(\sqrt{x^2+y^2}+itan^{-1}(\frac{y}{x})</math> adding integer multiples of <math>2\pi i</math> gives all the others. | <math>ln(z)= w = ln(|z|) + iarg(z) = ln(\sqrt{x^2+y^2}+itan^{-1}(\frac{y}{x})</math> adding integer multiples of <math>2\pi i</math> gives all the others. | ||
| − | *We can use COMPLEX function to convert real and imaginary number in to a complex number. | + | *We can use [[Manuals/calci/COMPLEX| COMPLEX]] function to convert real and imaginary number in to a complex number. |
==ZOS Section== | ==ZOS Section== | ||
Revision as of 02:58, 23 June 2014
IMLN(Complexnumber)
- is of the form
Description
- This function gives the Natural Logarithm of a complex number.
- In , where Complexnumber is in the form of . i.e & are the real numbers.
- And is the imaginary unit .
- Normally Complex logarithm function is an inverse of the Complex exponential function.
- A logarithm of is a complex number such that and it is denoted by .
- If with & are real numbers then natural logarithm of a complex number :
adding integer multiples of gives all the others.
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
ZOS Section
- The syntax is to calculate the natural logarithm of a complex number in ZOS is .
- is of the form
- For e.g.,IMLN(("10+17i")
Examples
- IMLN("3-2i")=1.28247467873077-0.588002603547568i
- IMLN("6+7i")=2.22132562824516+0.862170054667226i
- IMLN("4")=1.38629436111989 But calci is not considering the zero value of imaginary value of z.
- IMLN("10i")=2.30258509299405+1.5707963267949i
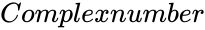 is of the form
is of the form 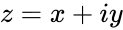
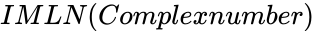 , where Complexnumber is in the form of
, where Complexnumber is in the form of  &
& 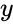 are the real numbers.
are the real numbers.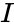 is the imaginary unit
is the imaginary unit 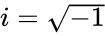 .
.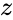 is a complex number
is a complex number 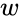 such that
such that 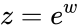 and it is denoted by
and it is denoted by 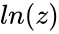 .
.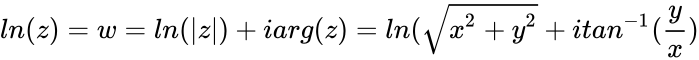 adding integer multiples of
adding integer multiples of 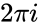 gives all the others.
gives all the others.