Difference between revisions of "Manuals/calci/NORMALDISTRIBUTED"
Jump to navigation
Jump to search
(Created page with "normal") |
|||
| Line 1: | Line 1: | ||
| − | normal | + | <div style="font-size:30px">'''NORMALDISTRIBUTED(x,m,sd)'''</div><br/> |
| + | *<math>x</math> is the value for which distribution is evaluated. | ||
| + | *<math>m </math> is the mean. | ||
| + | *<math>sd</math> is the standard deviation. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the value of the normal probability distribution. | ||
| + | *It is the continuous probability distribution. | ||
| + | *The normal distributions are a very important class of statistical distributions. | ||
| + | *All normal distributions are symmetric and have bell-shaped density curves with a single peak. | ||
| + | *The term bell curve is used to describe the mathematical concept called normal distribution. | ||
| + | *It is also called as Gaussian distribution. | ||
| + | *The Normal Distribution has: mean = median = mode | ||
| + | *i.e., This distribution is symmetry about the center. | ||
| + | *Half of values less than the mean and half of values greater than the mean. | ||
| + | *In a normal distribution the probability values are satisfying the following conditions: | ||
| + | 1. The total area under the curve is equal to 1 (100%) | ||
| + | 2. About 68% of the area under the curve falls within 1 standard deviation. | ||
| + | 3. About 95% of the area under the curve falls within 2 standard deviations. | ||
| + | 4. About 99.7% of the area under the curve falls within 3 standard deviations. | ||
| + | *In a normal distribution the mean =0 and standard deviation =1,then the distribution is called the standard normal distribution or the unit normal distribution, and a random variable with that distribution is a standard normal deviate. | ||
| + | *It is the only absolutely continuous distribution. | ||
| + | *A normal distribution is calculated by : | ||
| + | <math>f(x,\mu,\sigma)=\frac {1}{\sigma\sqrt{2\pi}} e^{\frac{-(x-\mu)^2}{2\sigma^2}}</math> | ||
| + | where <math>\mu</math> is the mean and <math>\sigma</math> is the standard deviaton of the distribution. | ||
| + | |||
| + | ==Examples== | ||
| + | #NORMALDISTRIBUTED(22,25,2.5) = -16.307435699813773,69.98317771544811,13.493570858283977,46.350299353375874 etc | ||
| + | #=NORMALDISTRIBUTED(30,36,20.9) = -39.85074927994863,24.24627001288364,23.575289380647483,-20.639707171803707,-8.8266089980268 etc. | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/NORMDIST | NORMDIST ]] | ||
| + | *[[Manuals/calci/NORMSDIST | NORMSDIST ]] | ||
| + | *[[Manuals/calci/NORMINV | NORMINV ]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://stattrek.com/probability-distributions/normal.aspx Normal Distribution] | ||
Revision as of 14:45, 14 December 2016
NORMALDISTRIBUTED(x,m,sd)
- is the value for which distribution is evaluated.
- is the mean.
- is the standard deviation.
Description
- This function gives the value of the normal probability distribution.
- It is the continuous probability distribution.
- The normal distributions are a very important class of statistical distributions.
- All normal distributions are symmetric and have bell-shaped density curves with a single peak.
- The term bell curve is used to describe the mathematical concept called normal distribution.
- It is also called as Gaussian distribution.
- The Normal Distribution has: mean = median = mode
- i.e., This distribution is symmetry about the center.
- Half of values less than the mean and half of values greater than the mean.
- In a normal distribution the probability values are satisfying the following conditions:
1. The total area under the curve is equal to 1 (100%) 2. About 68% of the area under the curve falls within 1 standard deviation. 3. About 95% of the area under the curve falls within 2 standard deviations. 4. About 99.7% of the area under the curve falls within 3 standard deviations.
- In a normal distribution the mean =0 and standard deviation =1,then the distribution is called the standard normal distribution or the unit normal distribution, and a random variable with that distribution is a standard normal deviate.
- It is the only absolutely continuous distribution.
- A normal distribution is calculated by :
where is the mean and is the standard deviaton of the distribution.
Examples
- NORMALDISTRIBUTED(22,25,2.5) = -16.307435699813773,69.98317771544811,13.493570858283977,46.350299353375874 etc
- =NORMALDISTRIBUTED(30,36,20.9) = -39.85074927994863,24.24627001288364,23.575289380647483,-20.639707171803707,-8.8266089980268 etc.
 is the value for which distribution is evaluated.
is the value for which distribution is evaluated.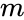 is the mean.
is the mean.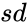 is the standard deviation.
is the standard deviation.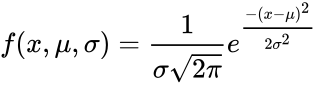 where
where 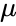 is the mean and
is the mean and 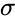 is the standard deviaton of the distribution.
is the standard deviaton of the distribution.